题目内容
12.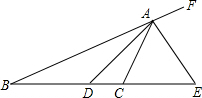 如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
分析 由AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,得出∠DAE=90°,进一步求得∠CAE=70°,利用三角形外角的性质得出∠ACD=∠E+∠CAE得出答案即可.
解答 解:∵AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,
∴∠DAE=$\frac{1}{2}$(∠BAC+∠CAF)=$\frac{1}{2}$×180°=90°,
∵∠DAC=∠BAD=20°,
∴∠CAE=70°,
∴∠ACD=∠E+∠CAE=50°+70°=120°.
点评 此题考查平角的意义,角平分线的性质,三角形外角的性质,结合图形,灵活运用已知条件,选择合适的方法解决问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
7.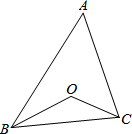 如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
 如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )| A. | 125° | B. | 115° | C. | 105° | D. | 95° |
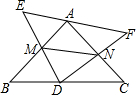 如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.
如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N. 如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.
如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.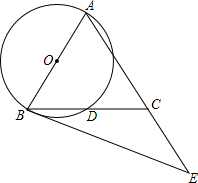 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.