题目内容
直线y=
x-2分别交x轴、y轴于A、B两点,O为坐标原点.
(1)点A的坐标为 ,点B的坐标为 ;
(2)过△AOB的顶点能不能画出一条直线把△AOB分成面积相等的两部分?若能,可以画出几条?它们有什么共同特点?并写出一条这样的直线的函数表达式;若不能,请说明理由.
| 2 |
| 3 |
(1)点A的坐标为
(2)过△AOB的顶点能不能画出一条直线把△AOB分成面积相等的两部分?若能,可以画出几条?它们有什么共同特点?并写出一条这样的直线的函数表达式;若不能,请说明理由.
考点:一次函数图象上点的坐标特征
专题:
分析:(1)令y=0求出x的值,再令x=0求出y的值即可得出A,B两点的坐标;
(2)根据三角形的中线把三角形的面积平分即可得出结论.
(2)根据三角形的中线把三角形的面积平分即可得出结论.
解答:解:(1)∵令y=0,则x=3;令x=0,则y=-2,
∴A(3,0),B(0,-2).
故答案为(3,0),(0,-2);
(2)能.
∵角形的中线把三角形的面积平分,
∴可以画三条,这三条直线都经过一个顶点和对边的中点.
∵A(3,0),B(0,-2),
∴AB的中点坐标D(
,-1),
设直线OD的解析式为y=kx(k≠0),
∴-1=
k,解得k=-
,
∴直线OD的解析式为y=-
x.
∴A(3,0),B(0,-2).
故答案为(3,0),(0,-2);
(2)能.
∵角形的中线把三角形的面积平分,
∴可以画三条,这三条直线都经过一个顶点和对边的中点.
∵A(3,0),B(0,-2),
∴AB的中点坐标D(
| 3 |
| 2 |
设直线OD的解析式为y=kx(k≠0),
∴-1=
| 3 |
| 2 |
| 2 |
| 3 |
∴直线OD的解析式为y=-
| 2 |
| 3 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
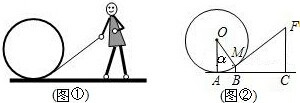 如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.
如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6. 在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=
在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=