题目内容
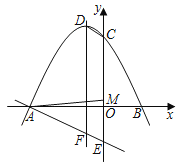
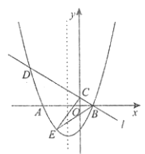
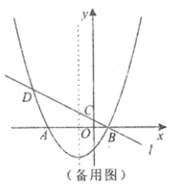
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() .
.
(1)则点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,抛物线的对称轴为__________;
的坐标为__________,抛物线的对称轴为__________;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,当
下方抛物线上的一点,当![]() 时.求
时.求![]() 面积的最大值;
面积的最大值;
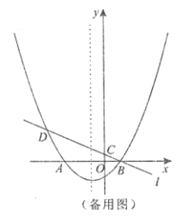
(3)设![]() 为抛物线对称轴上一点,点
为抛物线对称轴上一点,点![]() 在抛物线上,若以点
在抛物线上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形,求
为顶点的四边形为矩形,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,抛物线的对称轴是:直线
,抛物线的对称轴是:直线![]() ;(2)当
;(2)当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;(3)当点
;(3)当点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形时,
为顶点的四边形为矩形时,![]() 的值为
的值为![]() ,
,![]()
【解析】
(1)利用抛物线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,列方程直接求解,利用抛物线的对称轴公式直接求对称轴方程;
,列方程直接求解,利用抛物线的对称轴公式直接求对称轴方程;
(2)过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,利用
,利用![]() ,建立面积与
,建立面积与![]() 的横坐标的函数,利用函数的性质求最大值;
的横坐标的函数,利用函数的性质求最大值;
(3)分别以![]() 为边与对角线进行讨论,利用矩形的性质与抛物线的性质及平移的特点求解
为边与对角线进行讨论,利用矩形的性质与抛物线的性质及平移的特点求解![]() 的坐标,再利用函数知识或三角函数或相似建立方程即可得到答案.
的坐标,再利用函数知识或三角函数或相似建立方程即可得到答案.
解(1)令![]() ,得
,得![]() ,
,
因为:![]() ,所以
,所以![]() ,
,
所以:![]() ,
,
![]() ,
,![]() ,
,
抛物线的对称轴是:直线![]() ;
;
(2)过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
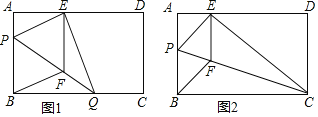
于点![]() ,如图1,
,如图1,
∵![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() , 直线
, 直线![]() 的解析式为
的解析式为![]()
设点![]() ,则
,则![]()
∴![]()
![]()
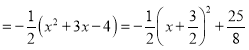
∵![]() ,∴当
,∴当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() .
.
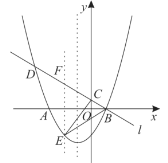
图1
(3)联立: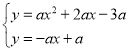 ,得
,得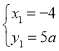 ,
,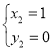
∴点![]()
①若点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的矩形中
为顶点的矩形中![]() ,
,
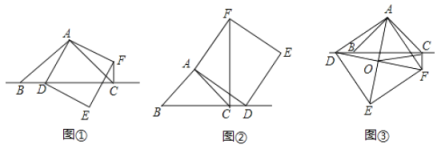
过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 于点
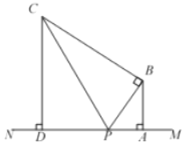
于点![]() 如图2,
如图2,
则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
由平移得,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() (负值合去)
(负值合去)
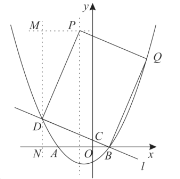
图2
②若矩形![]() 中
中![]() 为对角线,∵
为对角线,∵![]() ,
,![]() ,
,
由![]() ,
,
则由平移可得:点![]() 的坐标为
的坐标为![]() ,
,
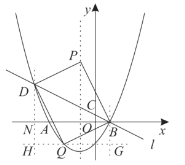
过点![]() 作
作![]() 轴,点
轴,点![]() 作
作![]() 轴,
轴,
过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,如图3,
,如图3,
则![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() (负值舍去)
(负值舍去)
∴当点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形时,
为顶点的四边形为矩形时,![]() 的值为
的值为![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
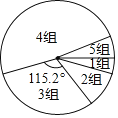
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.