题目内容
【题目】如图,在等腰![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连结
,连结![]() .
.
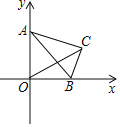
(猜想)如图①,当点![]() 在线段
在线段![]() 上时,直接写出
上时,直接写出![]() 、
、![]() 、
、![]() 三条线段的数量关系.
三条线段的数量关系.
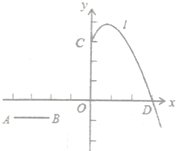
(探究)如图②,当点![]() 在线段
在线段![]() 的延长线上时,判断
的延长线上时,判断![]() 、
、![]() 、
、![]() 三条线段的数量关系,并说明理由.
三条线段的数量关系,并说明理由.
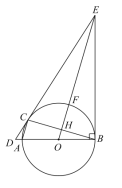
(应用)如图③,当点![]() 在线段
在线段![]() 的反向延长线上时,点
的反向延长线上时,点![]() 、
、![]() 分别在直线
分别在直线![]() 两侧,
两侧,![]() 、
、![]() 交点为点
交点为点![]() 连结
连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() .
.
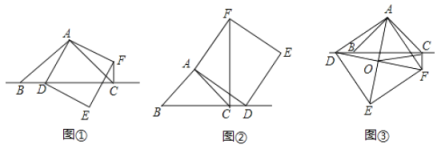
【答案】[猜想]![]() ;[探究]
;[探究]![]() ,理由见解析;[应用]
,理由见解析;[应用]![]()
【解析】
[猜想]根据正方形的性质得到∠BAC=∠DAF=90°,推出![]() ,根据全等三角形的性质即可得到结论;
,根据全等三角形的性质即可得到结论;
[探究]根据正方形的性质得到∠BAC=∠DAF=90°,推出![]() ,根据全等三角形的性质可得到结论.
,根据全等三角形的性质可得到结论.
[应用]根据题意计算出BC的值,通过![]() 得到
得到![]() ,由勾股定理得出DF的值,再由直角三角形斜边上的中线的性质得到CO的值即可.
,由勾股定理得出DF的值,再由直角三角形斜边上的中线的性质得到CO的值即可.
[猜想]![]() .证明如下:
.证明如下:
![]() 是等腰直角三角形.
是等腰直角三角形.
![]() .
.
![]() 四边形
四边形![]() 为正方形
为正方形
![]() ,
,![]()
又![]()
![]()
在![]() 和
和![]() 中
中
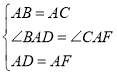
![]()
![]() ,
,![]()
[探究]
![]() 是等腰直角三角形.
是等腰直角三角形.
![]() .
.
![]() 四边形
四边形![]() 为正方形
为正方形
![]() ,
,![]()
又![]()
![]()
在![]() 和
和![]() 中
中
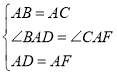
![]()
![]() ,
,
![]()
[应用]
同理可得![]()
![]() ,
,![]() ,
,![]() ,
,![]()
在![]() 中,
中,
![]()
![]()
![]()
∴![]()
∵![]()
![]()
在正方形![]() 中,
中,![]() 为
为![]() 中点
中点
∴在![]() 中,
中,![]()
![]()
![]()
![]()

练习册系列答案
相关题目