题目内容
【题目】如图，直线l：
与
轴交于点A，将直线l绕点A顺时针旋转75°后，所得直线的解析式为（ ）
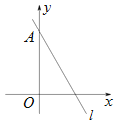
A.
B.
C.
D.
【答案】D
【解析】
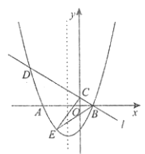
先求出直线l与坐标轴轴的交点A，B,再画出旋转后的直线AC，根据旋转角度75°可求得C点坐标，再利用待定系数法确定直线AC函数关系式.
如下图，设直线AC是直线l绕点A旋转75°后所得直线：
∵在直线l：
中，当
时，
；当
时，
，
∴点A的坐标为
，点B的坐标为（1，0），
∴OA=
，OB=1，
∵∠AOB=90°，∴AB=2=2OB，∴∠BAO=30°，
∵由题意可知∠BAC=75°，
∴∠OAC=45°，
∴△AOC是等腰直角三角形，
∴OC=OA=，
∴点C的坐标为
，
设直线AC的解析式为：
，则：
，解得
，
∴AC的解析式为：
.
故选D.
练习册系列答案
相关题目
