题目内容
9.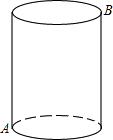 如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm.
如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm.
分析 要求最短路线,首先要把圆柱的侧面展开,利用两点间线段最短,再利用勾股定理来求.
解答  解:把圆柱侧面展开,展开图如右图所示,点A,B的最短距离为线段AB的长,
解:把圆柱侧面展开,展开图如右图所示,点A,B的最短距离为线段AB的长,
BC=6cm,AC为底面半圆弧长,AC=$\frac{8}{π}$•π=8,所以AB=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm).
故答案为:10cm.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.将下列长度的三根木棒首尾顺次连接,能组成三角形的是( )
| A. | 1,2,3 | B. | 3,4,5 | C. | 2,5,8 | D. | 3,6,9 |
17.某工厂现在平均每天比原计划多生产60台机器,现在生产900台机器所需时间与原计划生产750台机器所需时间相同.设原计划平均每天生产x台机器,则可列方程为( )
| A. | $\frac{900}{x}=\frac{750}{x+60}$ | B. | $\frac{900}{x+60}=\frac{750}{x}$ | C. | $\frac{900}{x}=\frac{750}{x-60}$ | D. | $\frac{900}{x-60}=\frac{750}{x}$ |
1.下列各式中运算正确的是( )
| A. | 2x+3y=5xy | B. | 5ab-5ba=0 | C. | 4a2-3a2=1 | D. | 2a2+2a3=2a5 |
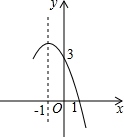 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: