题目内容
19．下列4个数中，$\sqrt{9}$，$\frac{22}{7}$，π，（$\sqrt{3}$）0，其中无理数是（ ）| A． | 9 | B． | $\frac{22}{7}$ | C． | π | D． | （$\sqrt{3}$）0 |
分析 根据无理数是无限不循环小数，可得答案．
解答 解：$\sqrt{9}$，$\frac{22}{7}$，（$\sqrt{3}$）0是有理数，
π是无理数，
故选：C．
点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．
练习册系列答案
初中学业考试导与练系列答案
相关题目
9．下列给出的式子一定是二次根式的是（ ）
| A． | $\sqrt{{a}^{2}-2}$ | B． | $\sqrt{{x}^{2}+2}$ | C． | $\sqrt{3-π}$ | D． | $\root{3}{a}$ |
10．若-2a＜-2b，则a＞b，则根据是（ ）
| A． | 不等式的基本性质1 | B． | 不等式的基本性质2 | ||
| C． | 不等式的基本性质3 | D． | 等式的基本性质2 |
7．不等式组$\left\{\begin{array}{l}{x+9＜5x+1}\\{x≥2x-3}\end{array}\right.$的解集是（ ）
| A． | x＞2 | B． | x≤3 | C． | 2＜x≤3 | D． | x≥3 |
14．点P在第二象限，若该点到x轴的距离为3，到y轴的距离为1，则点P的坐标是（ ）
| A． | （-1，3） | B． | （-3，1） | C． | （3，-1） | D． | （1，3） |
11．从一幅扑克牌中随机抽取一张牌，它是黑桃的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{5}$ | C． | $\frac{7}{27}$ | D． | $\frac{13}{54}$ |
8．
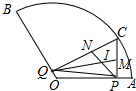扇形BOA的弧长为$\frac{4}{3}$π，面积为$\frac{4}{3}$π，在$\widehat{AB}$上取一点C，作CP⊥OA于P，CQ⊥OB于Q，△CPO的角平分线PN、QM交于I．当OP≤$\sqrt{3}$时，下列结论中错误的是（ ）
扇形BOA的弧长为$\frac{4}{3}$π，面积为$\frac{4}{3}$π，在$\widehat{AB}$上取一点C，作CP⊥OA于P，CQ⊥OB于Q，△CPO的角平分线PN、QM交于I．当OP≤$\sqrt{3}$时，下列结论中错误的是（ ）| A． | ⊙O半径为2 | B． | ∠PCQ=60° | C． | NQ+MP=$\sqrt{3}$ | D． | CN+CM=$\sqrt{3}$ |
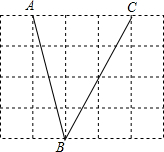如图，将线段AB放在边长为1的小正方形网格，点A点B均落在格点上，请只用一把无刻度直尺作图：①线段AB上画出点P，使AP=$\frac{\sqrt{17}}{3}$；②作△ABC，使点C落在格点上，并且使△ABC的面积为6（只作一个）；③作线段CD=$\frac{12\sqrt{17}}{17}$．