题目内容
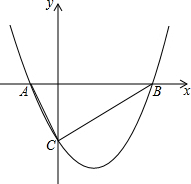 如图,抛物线y1=
如图,抛物线y1=| 1 |
| 2 |
(1)将抛物线y1向左平移1个单位,再向上平移m(m>0)个单位得到抛物线y2,若抛物线y2的顶点在△ABC内,则m的取值范围为
(2)在(1)的结论下,若抛物线y2上存在点Q,使得△QAC是以AC为底边的等腰三角形,则m的取值范围为
考点:二次函数图象与几何变换
专题:
分析:(1)首先根据平移确定平移后的函数的解析式,然后确定点P的坐标,然后求得点C的坐标,从而利用待定系数法确定直线AC的解析式,然后确定m的取值范围即可;
(2)求出AB中点,过此点且垂直于AB的直线在x=1的交点应该为顶点P的临界点,顶点P继续向上移动,不存在Q点,向下存在两个点P.
(2)求出AB中点,过此点且垂直于AB的直线在x=1的交点应该为顶点P的临界点,顶点P继续向上移动,不存在Q点,向下存在两个点P.
解答:解:(1)y=
x2-2x-6=
(x-2)2-8,
故抛物线的顶点坐标为(2,-8),
将求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1=
(x-2+1)2-8+m,
故P(1,-8+m),
在抛物线y=
x2-2x-6中易得C(0,-6),
当0=
x2-2x-6
解得:x1=-2,x2=6,
故B(6,0),
可得直线BC为y2=x-6,
当x=1时,y2=-5,
故-5<-8+m<0,
解得:3<m<8;
故答案为:3<m<8;
(2)∵C(0,-6),A(-2,0),
∴线段AC的中点坐标为(-1,-3),直线AC的解析式为y=-3x-6,
∴过AC的中点且与AC垂直的直线的解析式为:y=
x-
,
∴直线y=
x-
与y=
(x-1)2-8+m有交点,
联立方程,求得判别式为:
△=64-12(6m-29)≥0
解得:m≤
故①当3<m<
时,存在两个Q点,可作出两个等腰三角形;
②当m=
时,存在一个点Q,可作出一个等腰三角形;
③当
<m<8时,Q点不存在,不能作出等腰三角形,
综上所述:使得△QAC是以AC为底边的等腰三角形,则m的取值范围为3<m≤
.
故答案为:3<m≤
.
| 1 |
| 2 |
| 1 |
| 2 |
故抛物线的顶点坐标为(2,-8),
将求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1=
| 1 |
| 2 |
故P(1,-8+m),
在抛物线y=
| 1 |
| 2 |
当0=
| 1 |
| 2 |

解得:x1=-2,x2=6,
故B(6,0),
可得直线BC为y2=x-6,
当x=1时,y2=-5,
故-5<-8+m<0,
解得:3<m<8;
故答案为:3<m<8;
(2)∵C(0,-6),A(-2,0),
∴线段AC的中点坐标为(-1,-3),直线AC的解析式为y=-3x-6,
∴过AC的中点且与AC垂直的直线的解析式为:y=
| 1 |
| 3 |
| 8 |
| 3 |
∴直线y=
| 1 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
联立方程,求得判别式为:
△=64-12(6m-29)≥0
解得:m≤
| 103 |
| 18 |
故①当3<m<
| 103 |
| 18 |
②当m=
| 103 |
| 18 |
③当
| 103 |
| 18 |
综上所述:使得△QAC是以AC为底边的等腰三角形,则m的取值范围为3<m≤
| 103 |
| 18 |
故答案为:3<m≤
| 103 |
| 18 |
点评:本题考查了二次函数的综合知识,题目中还渗透了分类讨论的数学思想,这也是中考中常常出现的重要的数学思想,应加强此类题目的训练.

练习册系列答案
相关题目
若单项式3a m+
b2与abn-1的和也是单项式,则点P(m+1,n-2)所在象限为( )
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
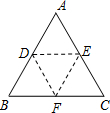 如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )
如图,折叠三角形纸片ABC,使点A落在BC边上的点F处,且折痕DE∥BC.若∠C=46°,则∠CFE=( )| A、43° | B、44° |
| C、45° | D、46° |
 如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB.
如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB. 全市七运会在塖州市举办,在800m比赛中,甲乙两名运动员同时起跑,刚跑出160m后,甲不慎摔得,他又迅速的爬起来继续投入比赛,并取得了优异的成绩.如图分别表示甲乙两名运动员所跑路程y(m)与比赛时间x(s)之间的关系,根据图象可得:甲摔倒后是在距离起点
全市七运会在塖州市举办,在800m比赛中,甲乙两名运动员同时起跑,刚跑出160m后,甲不慎摔得,他又迅速的爬起来继续投入比赛,并取得了优异的成绩.如图分别表示甲乙两名运动员所跑路程y(m)与比赛时间x(s)之间的关系,根据图象可得:甲摔倒后是在距离起点 已知直线a∥b,填空:图(1)中∠1=
已知直线a∥b,填空:图(1)中∠1=