题目内容
 如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB.
如图,在△ABC中,∠C=2∠B,D是BC边上一点,且AD⊥AB.(1)求证:BD=2AC;
(2)若∠C=45°,AD2=4-2
| 2 |
考点:相似三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)找到BD中点E,连接AE,易证AE=BE,AE=AC,即可解题;
(2)易证∠ADB=67.5°,即可求得AB2的值,再根据勾股定理即可求得BD的长,即可求得AC的长,易证△ACD∽△BCA,可得
=
,即可求得CD的长,即可解题.
(2)易证∠ADB=67.5°,即可求得AB2的值,再根据勾股定理即可求得BD的长,即可求得AC的长,易证△ACD∽△BCA,可得
| AC |
| BC |
| CD |
| AC |
解答:解:(1)找到BD中点E,连接AE,
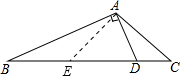
∵E是BD中点,
∴AE=BE,
∴∠B=∠BAE,
∴∠AEC=2∠B,
∵∠C=2∠B,
∴∠AEC=∠C,
∴AE=AC,
∴BD=2AC;
(2)∵∠C=45°,
∴∠B=22.5°,
∴∠ADB=67.5°,
∴AB2=AD2•tan67.5°=(4-2
)•(
+1)2=4+2
,
∵BD2=AB2+AD2=8,
∴BD=2
,
∴AC=
,
∵∠BAD=90°,
∴∠CAD=22.5°,
∴△ACD∽△BCA,
∴
=
,
∴CD(CD+2
)=2,
解得:CD=2-
.

∵E是BD中点,
∴AE=BE,
∴∠B=∠BAE,
∴∠AEC=2∠B,
∵∠C=2∠B,
∴∠AEC=∠C,
∴AE=AC,
∴BD=2AC;
(2)∵∠C=45°,
∴∠B=22.5°,
∴∠ADB=67.5°,
∴AB2=AD2•tan67.5°=(4-2
| 2 |
| 2 |
| 2 |
∵BD2=AB2+AD2=8,
∴BD=2
| 2 |
∴AC=
| 2 |
∵∠BAD=90°,
∴∠CAD=22.5°,
∴△ACD∽△BCA,
∴
| AC |
| BC |
| CD |
| AC |
∴CD(CD+2
| 2 |
解得:CD=2-
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ACD∽△BCA是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,已知∠AOB:∠BOC:∠COD=2:1:3,且∠AOC+∠DOB=150°,求∠AOD的度数.
如图,已知∠AOB:∠BOC:∠COD=2:1:3,且∠AOC+∠DOB=150°,求∠AOD的度数.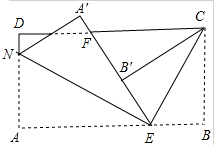 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.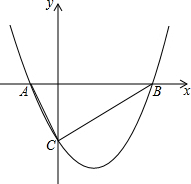 如图,抛物线y1=
如图,抛物线y1=