题目内容
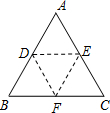如图，折叠三角形纸片ABC，使点A落在BC边上的点F处，且折痕DE∥BC．若∠C=46°，则∠CFE=（ ）| A、43° | B、44° |
| C、45° | D、46° |
考点：平行线的性质,翻折变换（折叠问题）
专题：
分析：根据两直线平行，同位角相等可得∠AED=∠C，再根据翻折的性质可得∠AED=∠DEF，然后根据两直线平行，内错角相等可得∠CFE=∠DEF．
解答：解：∵DE∥BC，
∴∠AED=∠C=46°，
由翻折的性质得，∠AED=∠DEF=46°，
∵DE∥BC，
∴∠CFE=∠DEF=46°．
故选D．
∴∠AED=∠C=46°，
由翻折的性质得，∠AED=∠DEF=46°，
∵DE∥BC，
∴∠CFE=∠DEF=46°．
故选D．
点评：本题考查了平行线的性质，翻折变换的性质，熟记各性质并准确识图理清图中各角度之间的关系是解题的关键．
练习册系列答案
相关题目
如图，已知∠AOB：∠BOC：∠COD=2：1：3，且∠AOC+∠DOB=150°，求∠AOD的度数．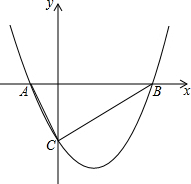
如图，抛物线y1=
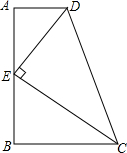如图，在四边形ABCD中，AD∥BC，E为AB的中点，DE⊥CE．
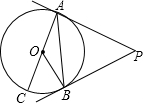（1）⊙O的直径为11cm，若圆心到一直线的距离为5.5cm，那么这条直线和圆的关系是