题目内容
13.先化简,再求值:(1)$\frac{{a}^{2}-8a+16}{{a}^{2}-16}$,其中a=5;
(2)$\frac{{a}^{2}+ab}{{a}^{2}+2ab+{b}^{2}}$,其中a=3b≠0.
分析 (1)根据平方差公式和完全平方公式可以化简题目中的式子,然后将a的值代入化简后的式子即可解答本题;
(2)根据提公因式法和完全平方公式可以化简题目中的式子,然后将a=3b≠0代入化简后的式子即可解答本题.
解答 解:(1)$\frac{{a}^{2}-8a+16}{{a}^{2}-16}$
=$\frac{(a-4)^{2}}{(a+4)(a-4)}$
=$\frac{a-4}{a+4}$,
当a=5时,原式=$\frac{5-4}{5+4}=\frac{1}{9}$;
(2)$\frac{{a}^{2}+ab}{{a}^{2}+2ab+{b}^{2}}$
=$\frac{a(a+b)}{(a+b)^{2}}$
=$\frac{a}{a+b}$,
当a=3b≠0时,原式=$\frac{3b}{3b+b}=\frac{3b}{4b}=\frac{3}{4}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
3.一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )


| A. | 2018 | B. | 2017 | C. | 2016 | D. | 2015 |
3.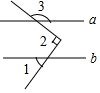 如图,已知a∥b,∠1=55°,∠2=90°,则∠3的度数为( )
如图,已知a∥b,∠1=55°,∠2=90°,则∠3的度数为( )
 如图,已知a∥b,∠1=55°,∠2=90°,则∠3的度数为( )
如图,已知a∥b,∠1=55°,∠2=90°,则∠3的度数为( )| A. | 35° | B. | 55° | C. | 125° | D. | 145° |
 如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.