题目内容
14.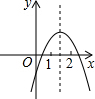 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由抛物线开口向下得到a<0,由对称轴在x=1的右侧得到-$\frac{b}{2a}$>1,于是利用不等式的性质得到2a+b>0;由a<0,对称轴在y轴的右侧,a与b异号,得到b>0,抛物线与y轴的交点在x轴的下方得到c<0,于是abc>0;抛物线与x轴有两个交点,所以△=b2-4ac>0;由x=1时,y>0,可得a+b+c>0;由x=-2时,y<0,可得4a-2b+c<0.
解答 解:①∵抛物线开口向下,
∴a<0,
∵对称轴x=-$\frac{b}{2a}$>1,
∴2a+b>0,故①正确;
②∵a<0,-$\frac{b}{2a}$>0,
∴b>0,
∵抛物线与y轴的交点在x轴的下方,
∴c<0,
∴abc>0,故②错误;
③∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,故③正确;
④∵x=1时,y>0,
∴a+b+c>0,故④错误;
⑤∵x=-2时,y<0,
∴4a-2b+c<0,故⑤正确.
故选:B.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0)的图象,当a>0,开口向上,a<0,开口向下;对称轴为直线x=-$\frac{b}{2a}$,a与b同号,对称轴在y轴的左侧,a与b异号,对称轴在y轴的右侧;当c<0,抛物线与y轴的交点在x轴的下方;当△=b2-4ac>0,抛物线与x轴有两个交点.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
4.下列四个几何体:
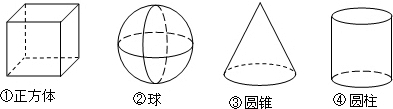
其中左视图与俯视图相同的几何体共有( )

其中左视图与俯视图相同的几何体共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.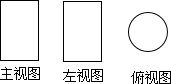 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )
 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )| A. | 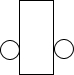 | B. | 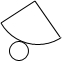 | C. | 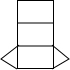 | D. | 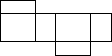 |
2.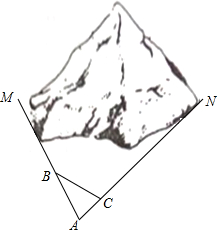 (1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(2)列方程(组)或不等式(组)解应用题:
2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%,求这份快餐最多含有多少克的蛋白质?
 (1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.(2)列方程(组)或不等式(组)解应用题:
2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
| 信息 1、快餐成分:蛋白质、脂肪、碳水化合物和其他 2、快餐总质量为400克 3、碳水化合物质量是蛋白质质量的4倍 |
9.直线y=2x-4与y轴的交点坐标是( )
| A. | (4,0) | B. | (0,4) | C. | (-4,0) | D. | (0,-4) |
6. 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
3.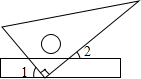 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )| A. | 52° | B. | 38° | C. | 42° | D. | 60° |
4.下列事件是必然事件的是( )
| A. | 地球绕着太阳转 | B. | 抛一枚硬币,正面朝上 | ||
| C. | 明天会下雨 | D. | 打开电视,正在播放新闻 |