题目内容
12.已知关于x的一元二次方程x2+(k-1)x+3=0两根的和为6,求k的值及方程的两根.分析 由关于x的一元二次方程x2+(k-1)x+3=0两根的和为6,根据根与系数的关系,可得-(k-1)=6,即可求得k的值,继而可得原方程为x2-6x+3=0,解此方程即可求得答案.
解答 解:∵关于x的一元二次方程x2+(k-1)x+3=0两根的和为6,
∴-(k-1)=6,
解得:k=-5,
∴原方程为:x2-6x+3=0,
∴x2-6x=-3,
∴x2-6x+9=-3+9,
∴(x-3)2=6,
解得:x1=$\sqrt{6}$+3,x2=-$\sqrt{6}$+3.
点评 此题考查了根与系数的关系以及一元二次方程的解法.注意若x1,x2是方程x2+px+q=0的两根时,则x1+x2=-p,x1x2=q.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
2.已知-1<a<0,点(a-2,y1),(a,y2),(a+2,y3)都在函数y=x2的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y3<y1<y2 |
3.下列说法错误的是( )
| A. | 一个四边形最多有三个锐角 | B. | 一个四边形最多有三个直角 | ||
| C. | 一个四边形最多有三个钝角 | D. | 一个四边形可能有一个锐角 |
1.下列各式中不是方程的是( )
| A. | 2x=1 | B. | 2x+y=3 | C. | 7+8=15 | D. | $\frac{1}{7}$x=2 |
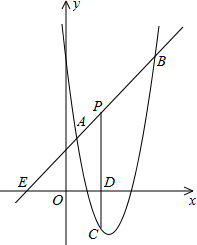 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.当△PAC为直角三角形时点P的坐标(3,5)或($\frac{7}{2}$,$\frac{11}{2}$).