题目内容
5. 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点.(1)求抛物线和直线AB的函数关系式;
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点.(1)求抛物线和直线AB的函数关系式;(2)P为线段OA上一个动点,点M为直线AB上一动点,若PM+CM的值最小,求M点和P点的坐标;
(3)P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.若△OPQ为直角三角形,试求点P的坐标.
分析 (1)根据抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点,设直线AB的函数关系式为y=kx+b,由直线AB交x轴于点A(-4,0),交y轴于点B(0,2),利用待定系数法即可求得抛物线和直线AB的函数关系式;
(2)连接CB并延长,使CB=BC′,过C′作CP⊥OA交AB于M,由$\frac{OA}{OB}=2,\frac{OB}{OC}=2$,得到△AOB∽△BOC,根据相似三角形的性质得到∠BAO=∠CBO,求得∠ABO+∠CBO=90°,于是得到AB⊥CC′,推出C与C′关于AB对称,证得C′P=PM+CM的最小值,根据平行线等分线段定理得到OP=OC=1,把x=-1代入y=$\frac{1}{2}$x+2得:y=$\frac{3}{2}$,即可得到结论;
(3)由△OPQ为直角三角形,则可判定∠PQO=90°,然后设AP=PQ=a,PO=4-a,由勾股定理可得方程:(4-a)2=a2+22,继而求得答案.
解答 解:(1)∵抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点,
∴设抛物线的解析式为:y=a(x+4)(x-1),
∴a=-$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{5}}\\{b=\frac{1}{5}}\\{c=2}\end{array}\right.$,
∴抛物线的函数关系式为y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2;
设直线AB的函数关系式为:y=kx+b,
∵点A(-4,0),点B(0,2),
∴$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AB的函数关系式为:y=$\frac{1}{2}$x+2;
(2)连接CB并延长,使CB=BC′,过C′作CP⊥OA交AB于M,
∵A(-4,0),点B(0,2),C(1,0),
∴OA=4,OB=2,OC=1,
∵$\frac{OA}{OB}=2,\frac{OB}{OC}=2$,
∵∠AOB=∠BOC=90°,
∴△AOB∽△BOC,
∴∠BAO=∠CBO,
∴∠ABO+∠CBO=90°,
∴AB⊥CC′,
∴C与C′关于AB对称,
∴C′P=PM+CM的最小值,
∵C′P⊥x轴,BO⊥x轴,
∴C′P∥BO,
∵BC=BC′,
∴OP=OC=1,
把x=-1代入y=$\frac{1}{2}$x+2得:y=$\frac{3}{2}$,
∴P(-1,0),M(-1,$\frac{3}{2}$);
(3)∵△OPQ为直角三角形,
①若∠POQ=90°,则点Q在y轴上,
∵Q为第二象限的一个动点,
∴矛盾,
∴∠POQ≠90°;
②若∠QPO=90°,
则PA=PQ<OQ,PO<OQ,
∵OQ=OB=2,PO<2,
∴OA=OP+PA<4,
∵OA=4,
∴矛盾,
∴∠QPO≠90°;
③若∠PQO=90°,设AP=PQ=a,PO=4-a,
∴(4-a)2=a2+22,
解得:a=$\frac{3}{2}$,
∴PO=4-a=$\frac{5}{2}$,
∴点P的坐标为:(-$\frac{5}{2}$,0).
点评 此题考查了待定系数法求二次函数和一次函数解析式,求点的坐标,相似三角形的判定和性质,轴对称的性质,直角三角形的性质.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

| A. | 抛一枚硬币,正面朝上 | |
| B. | 打开电视,正在播放动画片 | |
| C. | 3个人分成两组,每组至少1人,一定有2个人分在同一组 | |
| D. | 随意掷两个均匀的骰子,上面的点数之和为6 |
| A. | 9的算术平方根是3 | B. | $\sqrt{16}$的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
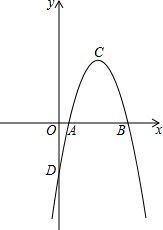 如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.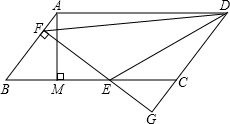 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( ) 如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$.
如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$.