题目内容
20.你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你一些原因和方法.(1)阅读下列材料
问题:利用一元一次方程将0.$\stackrel{•}{7}$化成分数.
解:设0.$\stackrel{•}{7}$=x
方程两边都乘以10,可得10×0.$\stackrel{•}{7}$=7.777…=7+0.$\stackrel{•}{7}$
即7+x=10x.(请你体会将方程两边都乘以10起到的作用)
可解得x=$\frac{7}{9}$,即0.$\stackrel{•}{7}$=$\frac{7}{9}$
(1)填空:将0.$\stackrel{•}{4}$写成分数形式为$\frac{4}{9}$.
(2)请你仿照上述方法把0.$\stackrel{•}{7}$$\stackrel{•}{3}$化成分数形式(要求写出利用一元一次方程进行解答的过程)
分析 (1)根据阅读材料设0.$\stackrel{•}{4}$=x,方程两边都乘以10,转化为4+x=10x,求出其解即可;
(2)设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=m,方程两边都乘以100,转化为73+m=100m,求出其解即可.
解答 解:(1)设0.$\stackrel{•}{4}$=x,则4+x=10x,
∴x=$\frac{4}{9}$.
故答案是:$\frac{4}{9}$;
(2)设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=m,方程两边都乘以100,可得100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=100m
由0.$\stackrel{•}{7}$$\stackrel{•}{3}$=0.7373…,可知100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=73.7373…=73+0.73
即73+m=100m,
可解得m=$\frac{73}{99}$,
即0.$\stackrel{•}{7}$$\stackrel{•}{3}$=$\frac{73}{99}$.
点评 本题考查了无限循环小数转化为分数的运用,运用一元一次方程解实际问题的运用,解答时根据等式的性质变形建立方程是解答的关键.

练习册系列答案
相关题目
10.若△ABC的三边a,b,c满足a2+b2-8a-10b+29+|c-3|=0,则( )
| A. | △ABC是直角三角形且∠C=90° | B. | △ABC是锐角三角形 | ||
| C. | △ABC是直角三角形且∠B=90° | D. | △ABC是直角三角形且∠A=90° |
5.有下列说法:(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数、零、负无理数;(4)无理数都可以用数轴上的点来表示.其中正确的说法的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.已知xy≠1,且有3x2+2014x+7=0,7y2+2014y+3=0,则$\frac{x}{y}$的值等于( )
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | -$\frac{2014}{7}$ | D. | -$\frac{2014}{3}$ |
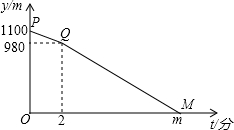 A、B相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t的函数关系式如图,回答下列问题
A、B相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t的函数关系式如图,回答下列问题 如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为120°.
如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为120°.