题目内容
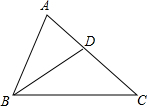
6. 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,∠DEF=∠A,EF与BD相交于点M,以下结论:①△BDE是等腰三角形;②四边形AFED是菱形;③BE=AF;④若AF:BF=3:4,则△DEM的面积:△BAD的面积=9:49,以上结论正确的是( )
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,∠DEF=∠A,EF与BD相交于点M,以下结论:①△BDE是等腰三角形;②四边形AFED是菱形;③BE=AF;④若AF:BF=3:4,则△DEM的面积:△BAD的面积=9:49,以上结论正确的是( )| A. | ①②③④ | B. | ①③④ | C. | ①③ | D. | ③④ |
分析 根据角平分线的性质得到∠DBE=∠ABD,根据平行线的性质得到∠ABD=∠BDE,等量代换得到∠DBE=∠BDE,于是得到△BDE是等腰三角形,故①正确;根据平行线的性质得到∠BAC+∠ADE=180°,得到EF∥AD,证得四边形ADEF为平行四边形,故②错误;等量代换得到BE=AF;故③正确;如图,连接DF,根据相似三角形的性质得到$\frac{{S}_{△DEM}}{{S}_{△BFM}}$=($\frac{DE}{BF}$)2=$\frac{9}{16}$,$\frac{EM}{FM}=\frac{DE}{BF}$=$\frac{3}{4}$,根据图象面积的和差得到△DEM的面积:△BAD的面积=9:49,故④正确.
解答 证明:∵BD是△ABC的角平分线,
∴∠DBE=∠ABD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
∴△BDE是等腰三角形,故①正确;
∵DE∥AB,
∴∠BAC+∠ADE=180°,
∵∠DEF=∠BAC,
∴∠DEF+∠ADE=180°,
∴EF∥AD,
∴四边形ADEF为平行四边形,故②错误;
∴AF=DE,
∴BE=AF;故③正确;
如图,连接DF,
∵DE∥AB,
∴△DEM∽△BFM,
∴$\frac{{S}_{△DEM}}{{S}_{△BFM}}$=($\frac{DE}{BF}$)2,
∵DE=AF,AF:BF=3:4,
∴$\frac{{S}_{△DEM}}{{S}_{△BFM}}$=($\frac{DE}{BF}$)2=$\frac{9}{16}$,$\frac{EM}{FM}=\frac{DE}{BF}$=$\frac{3}{4}$,
∴$\frac{{S}_{△DFM}}{{S}_{△DEM}}$=$\frac{4}{3}$,
∴S四边形AFMD=$\frac{11}{3}$S△DEM,S△BFM=$\frac{16}{9}$S△DEM,
∴△DEM的面积:△BAD的面积=9:49,故④正确,
故选B.
点评 本题考查了相似三角形的判定与性质:两个三角形相似对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.解决本题的关键是灵活应用平行线分线段成比例定理.

| A. | 图象的开口向下 | B. | 当x=2时,y有最大值-3 | ||
| C. | 图象的顶点坐标为(2,-3) | D. | 图象与y轴的交点坐标为(0,-3) |
| A. |  | B. |  | C. |  | D. |  |
 如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )| A. | y=x+2 | B. | y=2x+5 | C. | y=-x+4 | D. | y=-x+5 |
 如图,在△ABC中,点D在边AC上,∠ABD=∠ACB,如果S△ABD=4,S△BCD=5,CD=5,那么AB=6米.
如图,在△ABC中,点D在边AC上,∠ABD=∠ACB,如果S△ABD=4,S△BCD=5,CD=5,那么AB=6米. 如图,在平面直角坐标系xOy中,点A的坐标为(0,2),点B的坐标为(4,0),连接AB,作线段AB的垂直平分线l1,过点B作x轴的垂线l2,记l1,l2的交点为P.
如图,在平面直角坐标系xOy中,点A的坐标为(0,2),点B的坐标为(4,0),连接AB,作线段AB的垂直平分线l1,过点B作x轴的垂线l2,记l1,l2的交点为P.