题目内容

△ABC中，∠ACB=90°，CD是斜边上的高，AC=5，BC=12，则CD=
 
．
考点：勾股定理
专题：
分析：先根据勾股定理求出AB的长，再由三角形的面积公式即可得出CD的长．
解答：解：∵△ABC中，∠ACB=90°，AC=5，BC=12，
∴AB=
AC2+BC2
=
52+122
=13，
∴CD=
AC•BC
AB
=
5×12
13
=
60
13
．
故答案为：
60
13
．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
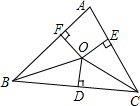如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF=OD=OE，若∠BAC=70°，∠BOC=
 
．
计算：
（1）12-（-18）+（-7）-15             
（2）（-48）÷8-（-25）×（-6）；
（3）-22+3×（-1）4-（-4）×5          
（4）-22÷（-4）3+|0.8-1|×（2
1
2
）2．
对π取近似数3.14，精确到
 
位．
计算（-7）×（-3）×（-56）×0÷（-13）=
 
，（-1）÷15×
1
15
=
 
，4910×（
1
49
）11=
 
；比较大小：-
2
3
 
-
3
4
．
在数0，π，0.1010010001…，
22
7
中无理数有
 
个．
|a+2|+（b-1）2=0，那么（a+b）2007的值是（　　）
A、-2007B、2007
C、-1D、1
某商店出售一种商品，其原价为m元，现有如下两种调价方案：一种是先提价5%，在此基础上又降价5%；另一种是先降价5%，在此基础上又提价5%．
（1）用这两种方案调价的结果是否一样？调价后的结果是不是都恢复了原价？试计算说明．
（2）两种调价方案改为：一种是先提价15%，在此基础上又降价15%；另一种是先降价15%，在此基础上又提价15%．这时结果怎样？试计算说明．
（3）你能总结出什么规律吗？
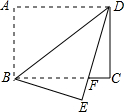如图，在长方形ABCD中，AB∥CD，AD∥BC，AB=3，BC=4，将矩形纸片沿BD折叠，使点A落在点E处．设DE与BC相交于点F，
（1）判断△BDF的形状，并说明理由；
（2）求DF的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网