题目内容
19.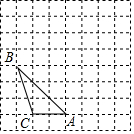 如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:(1)△ABC的顶点都在方格纸的格点上,先将△ABC向右平移2个单位,再向上平移3个单位,得到△A1B1C1,其中点A1、B1、C1分别是A、B、C的对应点,试画出
△A1B1C1;
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为平行,线段AA1、BB1的数量关系为相等;
(3)△A1B1C1的面积为3(平方单位)
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用平移的性质得出线段AA1、BB1的位置与数量关系;
(3)直接利用钝角三角形面积求法得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)线段AA1、BB1的位置关系为:平行,
线段AA1、BB1的数量关系为:相等;
故答案为:平行,相等;
(3)△A1B1C1的面积为:$\frac{1}{2}$×2×3=3.
故答案为:3.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
14.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角都是直角 | B. | 四条边相等 | C. | 对角线相等 | D. | 对角线互相平分 |
8. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
 如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.
如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.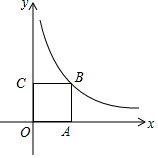 如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.
如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.