题目内容
8. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
分析 根据平行四边形的性质得出点B的横坐标,再由DB:DC=3:1得出点C的横坐标,由∠BAO=60°,得∠COD,即可得出点C坐标,即可得出k的值.
解答 解:∵四边形ABCD是平行四边形,点A的坐标为(-4,0),
∴BC=4,
∵DB:DC=3:1,
∴B(-3,OD),C(1,OD),
∵∠BAO=60°,
∴∠COD=30°,
∴OD=$\sqrt{3}$,
∴C(1,$\sqrt{3}$),
∴k=$\sqrt{3}$,
故选D.
点评 本题考查了平行四边形的性质,掌握平行四边形的性质以及反比例函数图象上点的坐标特征是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
16. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC
其中正确的是( )
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC
其中正确的是( )
| A. | ①②③④ | B. | ②③ | C. | ①②④ | D. | ①③④ |
13.已知A,B两点分别在反比例函数y=$\frac{3m}{x}$(m≠0)和y=$\frac{2m-5}{x}$(m≠$\frac{5}{2}$)的图象上,若点A与点B关于x轴对称,则m的值为1.
20.观察以下一列数的特点:0,1,-4,9,-16,25,…,则第11个数是( )
| A. | -121 | B. | -100 | C. | 100 | D. | 121 |
 如图,折叠一张长方形纸片,已知∠1=66°,则∠2的度数是57°.
如图,折叠一张长方形纸片,已知∠1=66°,则∠2的度数是57°.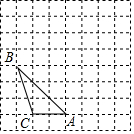 如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题: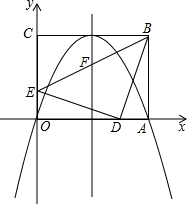 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).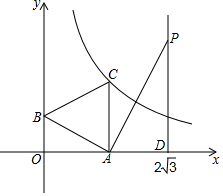 如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.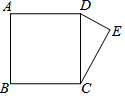 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE=12或5.
如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE=12或5.