题目内容
14. 在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).(1)请画出△ABC沿x轴向右平移4个单位长度后的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法)
(2)直接写出A′,B′,C′三点的坐标:A′(1,3),B′(0,1),C′(5,-2).
(3)求△ABC的面积.
分析 (1)将三点分别向右平移4个单位,再顺次连接即可得;
(2)由(1)中所画图形可得;
(3)割补法求解可得.
解答 解:(1)如图所示,△A′B′C′即为所求;
(2)三点的坐标为:A′(1,3),B′(0,1),C′(5,-2),
故答案为:1,3;0,1;5,-2.
(3)△ABC的面积为$\frac{1}{2}$×(1+5)×5-$\frac{1}{2}$×1×2-$\frac{1}{2}$×3×5=$\frac{13}{2}$.
点评 本题考查了坐标与图形的性质、三角形的面积问题,解题的关键是掌握直角坐标系中点的坐标的确定方法、分割法求三角形的面积的思想等知识点.

练习册系列答案
相关题目
9.不等式组$\left\{\begin{array}{l}{x+2≥0}\\{\frac{x}{2}-1<-\frac{1}{2}}\end{array}\right.$的解集在数轴上表示为( )
| A. |  | B. | 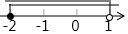 | C. | 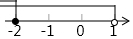 | D. |  |
3.在-1,$\frac{1}{3}$,$\sqrt{2}$,0.7中,无理数是( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\sqrt{2}$ | D. | 0.7 |
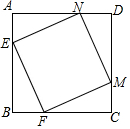 如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.
如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8. 如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$.
如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$.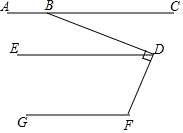 如图,已知AC∥ED,ED∥GF,∠BDF=90°.
如图,已知AC∥ED,ED∥GF,∠BDF=90°.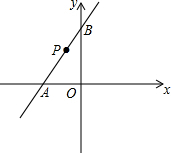 如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.