题目内容
1.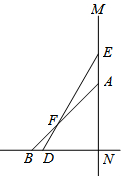 如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.
如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.(1)求∠BFD的度数;
(2)梯子底端向外移动了多少米?
分析 (1)直接利用三角形外角的性质得出∠BFD的度数;
(2)直接利用勾股定理得出BN的长,进而得出答案.
解答 解:(1)∵∠ABN+∠BFD=∠EDN=60°,∠ABN=45°,
∴∠BFD=60°-45°=15°;
(2)∵AB=DE=6m,∠EDN=60°,∠ABN=45°,
∴DN=3m,BN=AN,
∴BN2+AN2=AB2,
故2BN2=36,
解得:BN=3$\sqrt{2}$(m),
故BD=3($\sqrt{2}$-1)m,
答:梯子底端向外移动了3($\sqrt{2}$-1)米.
点评 此题主要考查了勾股定理的应用以及三角形的外角性质,正确得出三角形各边长是解题关键.

练习册系列答案
相关题目
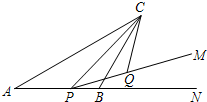 如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,∠CPM=30°,点Q是射线PM上的一个动点.则CQ长度的最小值是$\frac{5}{2}$.
如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,∠CPM=30°,点Q是射线PM上的一个动点.则CQ长度的最小值是$\frac{5}{2}$.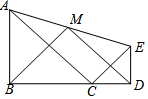 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,