题目内容
11.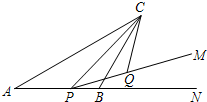 如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,∠CPM=30°,点Q是射线PM上的一个动点.则CQ长度的最小值是$\frac{5}{2}$.
如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,∠CPM=30°,点Q是射线PM上的一个动点.则CQ长度的最小值是$\frac{5}{2}$.
分析 根据题意可知:当CP确定时则当CQ⊥PM时,CQ最小,而CP最小时则CQ也最小,故当CP⊥AN时,CP最小,由直角三角形的性质和三角函数的定义可求得CP的最小值为5,可求得CQ最小值.
解答 解:由题意可知当CP最小时,可知在△CPQ中当CQ⊥PM时,CQ有最小值,
当CP⊥AN,CQ⊥PM时,如图,
∵在Rt△APC中,AC=10,∠BAC=30°,
∴PC=5,
∵在Rt△CPQ中,∠CPM=30°,
∴CQ=$\frac{1}{2}$CP=$\frac{5}{2}$,
则CQ的最小值是$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题主要考查直角三角形的性质及三角函数的定义,找到当CQ取得最小值时的点P和点Q的位置是解题的关键.

练习册系列答案
相关题目
20.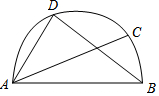 如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )
如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )
 如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )
如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 70° |
 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.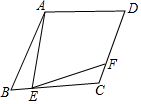 如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.
如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.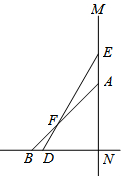 如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.
如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.