题目内容
16.我们都知道:|5-(-2)|表示5与-2之差的绝对值.实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:
(1)求|5-(-2)|=7.
(2)找出所有符合条件的整数x,使得|x+1|+|x-2|=3这样的整数是-1,0,1,2.
(3)由以上探索猜想对于任何有理数x,|x-3|+|x-6|的最小值是3.
分析 (1)利用绝对值的代数意义计算即可得到结果;
(2)找出满足已知等式的整数x的值即可;
(3)猜想得出原式的范围,即可确定出最小值.
解答 解:(1)原式=|5+2|=7;
(2)根据题意得:|x+1|+|x-2|=3这样的整数是-1,0,1,2;
(3)猜想|x-3|+|x-6|≥3,即最小值为3,
故答案为:(1)7;(2)-1,0,1,2;(3)3
点评 此题考查了整式的加减,弄清题中绝对值表示的意义是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.下列说法中正确的是( )
| A. | 2π是有理数 | B. | 数轴上表示-a的点一定在原点左边 | ||
| C. | 单项式-$\frac{2}{3}$πa2b的系数为-$\frac{2}{3}$ | D. | 多项式x-y的次数是1 |
6.下列属于一元二次方程是( )
| A. | 3x2-$\frac{2}{x}$=0 | B. | x2+2x+3 | C. | x(x-3)=0 | D. | (2x-1)2=4x(x-2) |
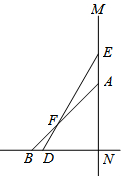 如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.
如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°. 甲,乙两只昆虫一开始在数轴上的点A,点B处,它们在数轴上所对应的数分别为-8,4;这两只昆虫各自以一定的速度在数轴上运动,且甲昆虫的运动速度为2个单位/秒.
甲,乙两只昆虫一开始在数轴上的点A,点B处,它们在数轴上所对应的数分别为-8,4;这两只昆虫各自以一定的速度在数轴上运动,且甲昆虫的运动速度为2个单位/秒.