题目内容
16.已知关于x的方程$\frac{x}{x+1}$+$\frac{x+1}{x}$=$\frac{4x+a}{x(x+1)}$只有一个实数根,求实数a的值.分析 分为两种情况,当△=0和△>0,再分别求出即可.
解答 解:去分母得整式方程,2x2-2x+1-a=0,△=4(2a-1),
(1)当△=0,即a=$\frac{1}{2}$时,显然x=$\frac{1}{2}$是原方程的解,
(2)当△>0,即a>$\frac{1}{2}$时,x1=$\frac{1}{2}$(1+$\sqrt{2a-1}$),x2=$\frac{1}{2}$(1-$\sqrt{2a-1}$),
显然x1>0,∴x1≠-1,x1≠0,它是原方程的解,
∴只需x2=0或-1时,x2为增根,此时原方程只有一个实数根,
∴当x2=0时,即$\frac{1}{2}$(1-$\sqrt{2a-1}$)=0,得:a=1;
当x2=-1时,即$\frac{1}{2}$(1-$\sqrt{2a-1}$)=-1,得:a=5,
综上,当a=$\frac{1}{2}$,1,5时原方程只有一个实数根.
点评 本题考查了解分式方程和分式有意义的条件,能求出符合的所有情况是解此题的关键.

练习册系列答案
相关题目
7.设m=8102-1902,则m用科学记数法表示为( )
| A. | 620×103 | B. | 62×104 | C. | 6.2×105 | D. | 0.62×106 |
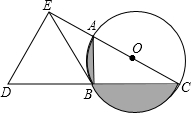 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.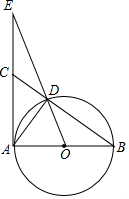 已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有①③④.
已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有①③④.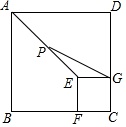 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.
如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为$\sqrt{5}$.