题目内容
15.若x2-5x-1=0,求①x2+$\frac{1}{{x}^{2}}$,②x4+$\frac{1}{{x}^{4}}$.分析 ①根据题意得到x-$\frac{1}{x}$=5,根据完全平方公式把原式化为(x-$\frac{1}{x}$)2+2,代入计算即可;
②把原式化为(x2+$\frac{1}{{x}^{2}}$)2-2,代入计算得到答案.
解答 解:∵x2-5x-1=0,
∴x-$\frac{1}{x}$=5,
①x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2=27;
②x4+$\frac{1}{{x}^{4}}$=(x2+$\frac{1}{{x}^{2}}$)2-2=727.
点评 本题考查的是完全平方公式,掌握(a±b)2=a2±2ab+b2是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在Rt△ABC中,若各边的长度都扩大2倍,则锐角A的四个三角比值( )
| A. | 也扩大2倍 | B. | 缩小为$\frac{1}{2}$倍 | ||
| C. | 都不变 | D. | 有的扩大,有的缩小 |
 一个正方体的每个面都写着一个汉字,其平面展开图如图所示,那么在该正方体中,和“曲”相对的汉字是( )
一个正方体的每个面都写着一个汉字,其平面展开图如图所示,那么在该正方体中,和“曲”相对的汉字是( )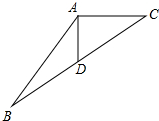 如图△ABC中,AB=10,AC=6,中线AD=4,则BC长是4$\sqrt{13}$.
如图△ABC中,AB=10,AC=6,中线AD=4,则BC长是4$\sqrt{13}$.
 如图所示,在△ABC中,∠B=60°,∠C=45°,AB=2$\sqrt{3}$,求AC的长.
如图所示,在△ABC中,∠B=60°,∠C=45°,AB=2$\sqrt{3}$,求AC的长.