题目内容
18. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CE的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CE的长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 连接CE,由旋转的性质得AD=AB=1、∠BAC=∠DAE=90°,结合∠B=60°知△ADB为等边三角形、AC=ABtanB=$\sqrt{3}$,再证△AEC是等边三角形可得CE=AE=AC=$\sqrt{3}$.
解答 解:如图,连接CE,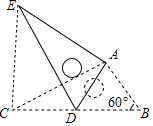
∵△ABC绕点A按顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上,
∴AD=AB=1,∠BAC=∠DAE=90°,
∵∠B=60°,
∴△ADB为等边三角形,AC=ABtanB=$\sqrt{3}$,
∵∠B=∠ADE=∠BAD=60°,
∴∠CAD=30°,
∴∠EAC=60°,
∵AE=AC=$\sqrt{3}$,
∴△AEC是等边三角形,
∴CE=$\sqrt{3}$,
故选:C.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质与解直角三角形的应用.

练习册系列答案
相关题目
13.64的算术平方根是( )
| A. | 8 | B. | ±2 | C. | ±8 | D. | 4 |
10.将抛物线y=$\frac{1}{2}$x2向左平移一个单位,所得抛物线的解析式为( )
| A. | y=$\frac{1}{2}$x2+1 | B. | y=$\frac{1}{2}$x2-1 | C. | y=$\frac{1}{2}$(x+1)2 | D. | y=$\frac{1}{2}$(x-1)2 |
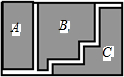 如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.
如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.