题目内容
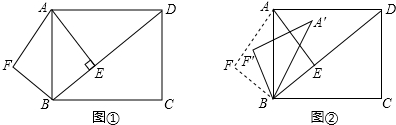
7.菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系CE+CF=$\frac{1}{2}$AB.;
(2)如图1,当∠ABC=90°时,若AC=4$\sqrt{2}$,BE=$\frac{3}{2}$,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
分析 (1)如图1中,连接EF,在CO上截取CN=CF,只要证明△OFN≌△EFC,即可推出CE+CF=OC,再证明OC=$\frac{1}{2}$AB即可.
(2)在Rt△CEF中,根据CE2+CF2=EF2即可解决问题.
(3)结论:CF-CE=$\sqrt{2}$O′C,过点O′作O′H⊥AC交CF于H,只要证明△FO′H≌△EO′C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
解答 解(1)结论CE+CF=$\frac{1}{2}$AB.
理由:如图1中,连接EF,在CO上截取CN=CF.
∵∠EOF+∠ECF=180°,
∴O、E、C、F四点共圆,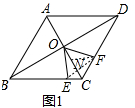
∵∠ABC=60°,四边形ABCD是菱形,
∴∠BCD=180°-∠ABC=120°,
∴∠ACB=∠ACD=60°,
∴∠OEF=∠OCF,∠OFE=∠OCE,
∴∠OEF=∠OFE=60°,
∴△OEF是等边三角形,
∴OF=FE,
∵CN=CF,∠FCN=60°,
∴△CFN是等边三角形,
∴FN=FC,∠OFE=∠CFN,
∴∠OFN=∠EFC,
在△OFN和△EFC中,
$\left\{\begin{array}{l}{FO=FE}\\{∠OFN=∠EFC}\\{FN=FC}\end{array}\right.$,
∴△OFN≌△EFC,
∴ON=EC,
∴CE+CF=CN+ON=OC,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠CBO=30°,AC⊥BD,
在RT△BOC中,∵∠BOC=90°,∠OBC=30°,
∴OC=$\frac{1}{2}$BC=$\frac{1}{2}$AB,
∴CE+CF=$\frac{1}{2}$AB.
(2)连接EF
∵在菱形ABCD中,∠ABC=90°,
∴菱形ABCD是正方形,
∴∠BOC=90°,OB=OC,AB=AC,∠OBE=∠OCF=45°,∠BCD=90°
∵∠EOF+∠BCD=180°,
∴∠EOF=90°,
∴∠BOE=∠COF
∴△OBE≌△OCF,
∴BE=CF,
∵BE=$\frac{3}{2}$,
∴CF=$\frac{3}{2}$,
在Rt△ABC中,AB2+BC2=AC2,AC=4$\sqrt{2}$
∴BC=4,
∴CE=$\frac{5}{2}$,
在Rt△CEF中,CE2+CF2=EF2,
∴EF=$\frac{\sqrt{34}}{2}$
答:线段EF的长为$\frac{\sqrt{34}}{2}$,
(3)结论:CF-CE=$\sqrt{2}$O′C.
理由:过点O′作O′H⊥AC交CF于H,
∵∠O′CH=∠O′HC=45°,
∴O′H=O′C,
∵∠FO′E=∠HO′C,
∴∠FO′H=∠CO′E,
∵∠EO′F=∠ECF=90°,
∴O′、C、F、E四点共圆,
∴∠O′EF=∠O′CF=45°,
∴∠O′FE=∠O′EF=45°,
∴O′E=O′F,
在△FO′H和△EO′C中,
$\left\{\begin{array}{l}{FO′=O′E}\\{∠FO′H=∠EO′C}\\{O′H=O′C}\end{array}\right.$,
∴△FO′H≌△EO′C,
∴FH=CE,
∴CF-CE=CF-FH=CH=$\sqrt{2}$O′C.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理、四点共圆等知识,解题的关键是发现四点共圆,添加辅助线构造全等三角形,属于中考压轴题.

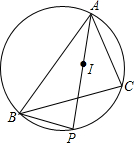 如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )
如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )| A. | $\frac{5}{2}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{25}{2}$ |
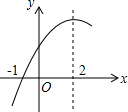 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
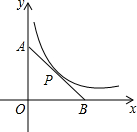 如图,A(0,2),B(2,0),双曲线y=$\frac{k}{x}$经过线段AB的中点P,则k的值是1.
如图,A(0,2),B(2,0),双曲线y=$\frac{k}{x}$经过线段AB的中点P,则k的值是1.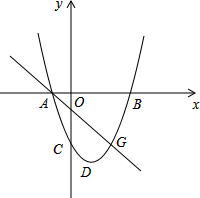 如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.