题目内容
7.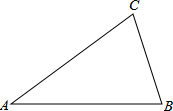 如图,已知△ABC.
如图,已知△ABC.(1)实践与操作:
利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作BC边上的高AD;
②作△ABC的角平分线BE;
(2)综合与运用;
若△ABC中,AB=AC且∠CAB=36°,
请根据作图和已知写出符合括号内要求的正确结论;
结论1:∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD;(关于角)
结论2:BD=DC,AE=BE,BC=BE;(关于线段)
结论3:△ABE,△BCE都是等腰三角形.(关于三角形)
分析 (1)①作BC边上的高AD,按照过直线外一点作直线的垂线步骤作即可;
②作△ABC的角平分线BE,按照作一个角的平分线的作法来做即可;
(2)根据等腰三角形的判定与性质结合(1)中的图形即可求解.
解答 解:(1)①②如图:
(2)∵AB=AC且∠CAB=36°,
∴∠ABC=∠C=72°,
∵BE是△ABC的角平分线,
∴∠ABE=∠CBE=36°,
∴∠ABE=∠CBE=∠CAB=36°.
∵AD是BC边上的高,AB=AC,
∴BD=DC,∠BAD=∠CAD.
∵∠EAB=∠ABE=36°,∠C=∠CEB=72°,
∴AE=BE,BC=BE,
∴△ABE,△BCE都是等腰三角形.
则结论1:∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);
结论2:BD=DC,AE=BE,BC=BE(关于线段);
结论3:△ABE,△BCE都是等腰三角形(关于三角形).
故答案为∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).
点评 本题主要考查过直线外一点作直线的垂线和作一个角的平分线的作法,也考查了等腰三角形的判定与性质.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案某公司为了更好得节约能源,决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备,其中每台的价格、工作量如下表。经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.
甲型 | 乙型 | |
价格(万元/台) |
|
|
产量(吨/月) | 240 | 180 |
(1)求a, b的值;
(2)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.


 有意义,则x的取值范围是 .
有意义,则x的取值范围是 .
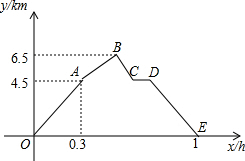 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.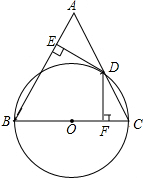 如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.