题目内容
11. 如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.
如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.(1)当四边形EPQD为矩形时,求t的值.
(2)当以点E、P、C、Q为顶点的四边形是平行四边形时,求t的值;
(3)探索:是否存在这样的t值,使三角形PDQ是以PD为腰的等腰三角形?若存在,求出t的值,若不存在,请说明理由.
分析 (1)首先过点C作CF⊥AB于点F,可得AE=BF=3cm,由AB∥CD,∠DEF=90°,可得当EP=DQ时,四边形EPQD为矩形,即可得方程:2t-3=10-t,解此方程即可求得答案;
(2)由AB∥CD,可得当AP=CQ时,以点E、P、C、Q为顶点的四边形是平行四边形,然后分别从当P在AE左侧时与当P在AE右侧时去分析求解即可求得答案;
(3)首先由勾股定理表示出PD2,DQ2,PQ2,然后分别从PD=DQ或PD=PQ去分析求解即可求得答案.
解答 解:(1)过点C作CF⊥AB于点F,
∵在等腰梯形ABCD中,AB∥DC,DE⊥AB,
∴DE=CF,
在Rt△ADE和Rt△BCF中,
$\left\{\begin{array}{l}{DE=CF}\\{AD=BC}\end{array}\right.$,
∴Rt△ADE≌Rt△BCF(HL);
∴BF=AE,
∵AB=16cm,CD=10cm,
∴AE=BF=3cm,
根据题意得:AP=2tcm,CQ=tcm,
∴EP=AP-AE=2t-3(cm),DQ=CD-CQ=10-t(cm),
∵AB∥CD,∠DEF=90°,
∴当EP=DQ时,四边形EPQD为矩形,
∴2t-3=10-t,
解得:t=$\frac{13}{3}$,
∴当四边形EPQD为矩形时,t=$\frac{13}{3}$;
(2)∵AB∥CD,
∴当AP=CQ时,以点E、P、C、Q为顶点的四边形是平行四边形,
当P在AE左侧时,EP=AE-AP=3-2t(cm),
此时3-2t=t,解得:t=1,
当P在AE右侧时,EP=AP-AE=2t-3(cm), 此时2t-3=t,解得:t=3,
此时2t-3=t,解得:t=3,
∴当以点E、P、C、Q为顶点的四边形是平行四边形时,t=1或t=3;
(3)存在.
理由:在Rt△ADE中,AE=3,AD=5,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=4,
∴PD2=PE2+DE2=(2t-3)2+42=4t2-12t+25,DQ2=(10-t)2=t2-20t+100,
过点Q作QM⊥AB于点M,则BM=BF+FM=3+t,
∴PM=AB-AP-BM=13-3t(cm),
∴PQ2=QM2+PM2=(13-3t)2+42=9t2-78t+185,
若PD=DQ,则4t2-12t+25=t2-20t+100,
解得:t=$\frac{-4±\sqrt{241}}{3}$(负值舍去);
若PD=PQ,则4t2-12t+25=9t2-78t+185,
解得:t1=$\frac{16}{5}$,t2=10(舍去),
综上可得:t=$\frac{16}{5}$或t=$\frac{-4+\sqrt{241}}{3}$.
点评 此题属于四边形的综合题,考查了平行四边形的判定与性质、等腰三角形的性质、矩形的判定与性质以及勾股定理等知识.注意掌握辅助线的作法,注意利用方程思想求解是解此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. |  | B. |  | C. |  | D. |  |
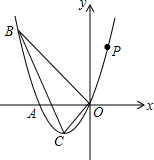 如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C. 如图,AB∥CD,EF交AB于点G,交CD与点F,FH交AB于点H,∠AGE=70°,∠BHF=125°,FH平分∠EFD吗?请说明你的理由.
如图,AB∥CD,EF交AB于点G,交CD与点F,FH交AB于点H,∠AGE=70°,∠BHF=125°,FH平分∠EFD吗?请说明你的理由.