题目内容
19.一个不透明的袋子中装有2个白球,1个红球,1个黑球,每个球除颜色外都相同,将球搅匀.(1)从中任意摸出1个球,恰好摸到白球的概率是$\frac{1}{2}$;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,求两次都摸到白球的概率.
(用树状图或列表法求解).
分析 (1)根据4个小球中白球的个数,即可确定出从中任意摸出1个球,恰好摸到白球的概率;
(2)列表得出所有等可能的情况数,找出两次都摸到白球的情况数,即可求出所求的概率.
解答 解:(1)4个小球中有2个白球,
则任意摸出1个球,恰好摸到白球的概率$\frac{1}{2}$,
故答案为:$\frac{1}{2}$;
(2)列表如下:
| 白 | 白 | 红 | 黑 | |
| 白 | --- | (白,白) | (白,红) | (黑,白) |
| 白 | (白,白) | --- | (白,红) | (黑,白) |
| 红 | (红,白) | (红,白) | --- | (黑,红) |
| 黑 | (白,黑) | (白,黑) | (红,黑) | --- |
则P(两次摸到白球)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了列表法与树状图法,以及概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
9. 某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
请根据所给的信息,解答下列问题:
(1)a=60,b=0.15;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人?
 某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 20 | 0.10 |
| 70≤x<80 | 30 | b |
| 80≤x<90 | a | 0.30 |
| 90≤x≤100 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人?
10.等腰三角形的一边为6,另一边为13,则它的周长为( )
| A. | 19 | B. | 25或32 | C. | 25 | D. | 32 |
4.为了清楚地反映部分占总体的百分比是多少,我们常选用的统计图是( )
| A. | 扇形图 | B. | 折线图 | C. | 条形图 | D. | 直方图 |
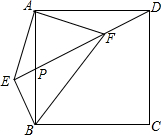 如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.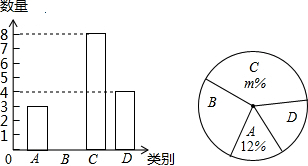
 如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.
如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒. 如图,D、E、F是正△ABC各边上的点,沿EF折叠后A与D重合,BD<DC,则图中相等的角有8对.
如图,D、E、F是正△ABC各边上的点,沿EF折叠后A与D重合,BD<DC,则图中相等的角有8对.