题目内容
16.先化简,再求值:$\frac{x+2}{{2{x^2}-4x}}÷(x-2+\frac{8x}{x-2})$,其中x=1.分析 先算括号里面的,再算除法,最后把x=1代入进行计算即可.
解答 解:原式=$\frac{x+2}{2x(x-2)}$÷$\frac{{x}^{2}+4-4x+8x}{x-2}$
=$\frac{x+2}{2x(x-2)}$÷$\frac{{x}^{2}+4+4x}{x-2}$
=$\frac{x+2}{2x(x-2)}$•$\frac{x-2}{(x+2)^{2}}$
=$\frac{1}{2x(x+2)}$,
当x=1时,原式=$\frac{1}{2×(1+2)}$=$\frac{1}{6}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.为了清楚地反映部分占总体的百分比是多少,我们常选用的统计图是( )
| A. | 扇形图 | B. | 折线图 | C. | 条形图 | D. | 直方图 |
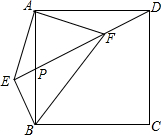 如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=$\sqrt{2}$AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个. 如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.
如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.