题目内容
11.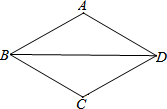 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
分析 分点Q在BC上和在CD上两种情况,根据直角三角形的性质和等腰三角形的性质解答即可.
解答 解:a、 如图1,
如图1,
∵AB=AD,∠BAD=120°,
∴∠ABD=30°,
∵△ABD≌△CBD,
∴∠CBD=30°,
∵AD∥BC,AQ⊥AD,
∴∠PQB=90°,又∠CBD=30°,PQ=2,
∴BP=4,
b、如图2,
由a得,PD=4,
则DQ=2$\sqrt{3}$,
∵∠BAD=120°,AB⊥AQ,
∴∠DAQ=30°,
∴AD=4$\sqrt{3}$,
则BD=12,
则BP=12-4=8,
∴BP的值为4或8,
故答案为:4或8.
点评 本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.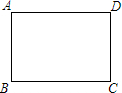 如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5.
如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.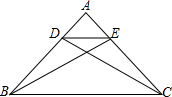 如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.
如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.