题目内容
4.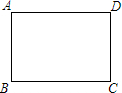 如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5.
如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5.
分析 四边形ABCD是矩形,则△ABC是直角三角形.根据勾股定理得到:AC=5,点B、C、D中只有两点在⊙A内,由题意可知一定是B在圆内,则半径r>3,一定是点C在圆外,则半径r<5,所以3<r<5.
解答 解:∵AB=3,AD=4,
∴AC=5,
∴点C一定在圆外,点B一定在圆内,
∴⊙A的半径r的取值范围是:3<r<5.
故答案为:3<r<5.
点评 本题主要考查了勾股定理,以及点和圆的位置关系,可以通过点到圆心的距离与圆的半径比较大小,判定点和圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
16.下列说法正确的是( )
| A. | 零是正数不是负数 | B. | 零既不是正数也不是负数 | ||
| C. | 零既是正数也是负数 | D. | 正数,负数和零统称有理数 |
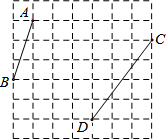 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.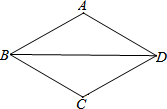 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.