题目内容
20.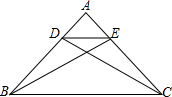 如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.
如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.
分析 根据已知条件得到∠AEB=∠ADC=90°,推出△ABE≌△ACD,根据全等三角形的性质得到AD=AE,由等腰三角形的性质得到∠ADE=∠AED=$\frac{180°-∠A}{2}$,∠AB=∠ACB=$\frac{180°-∠A}{2}$,等量代换得到∠ADE=∠ABC,然后由平行线的判定即可得到结论.
解答 证明:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中,$\left\{\begin{array}{l}{∠A=∠A}\\{∠AEB=∠ADC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD,
∴AD=AE,
∴∠ADE=∠AED=$\frac{180°-∠A}{2}$,
∵∠AB=∠ACB=$\frac{180°-∠A}{2}$,
∴∠ADE=∠ABC,
∴DE∥BC.
点评 本题考查了全等三角形的判定和性质,平行线的判定,垂直的定义.思路掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.下列函数(1)y=x;(2)y=2x-1;(3)y=$\frac{1}{x}$;(4)x+y=1中,是一次函数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
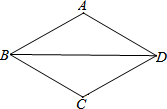 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.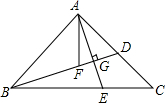 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由. 如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.
如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF. 如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC.
如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC. 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8. 的是( )
的是( ) B.
B.  C.
C.  D.
D. 