题目内容
4. 张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,S有最大值?并求出最大值?
分析 (1)设AB边的长为x米,则BC=32-2x,然后利用矩形的面积公式列出函数关系式即可;
(2)利用二次函数的性质求最大值即可.
解答 解:(1)由题意,得S=AB•BC=x(32-2x),
∴S=-2x2+32x(0<x<16).
(2)∵a=-2<0,
∴S有最大值.
∴x=-$\frac{b}{2a}$=-$\frac{32}{2×(-2)}$=8时,有S最大=$\frac{4ac-{b}^{2}}{4a}$=$\frac{-3{2}^{2}}{4×(-2)}$=128.
∴x=8时,S有最大值,最大值是128平方米.
点评 本题主要考查的是二次函数的应用,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
15.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
19.关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式等于4,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
16.下列说法正确的是( )
| A. | 零是正数不是负数 | B. | 零既不是正数也不是负数 | ||
| C. | 零既是正数也是负数 | D. | 正数,负数和零统称有理数 |
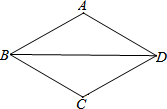 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.