题目内容
一元二次方程ax2+bx+c=0中,若a>0,b<0,c<0,则这个方程根的情况是( )
| A、有两个正根 |
| B、有两个负根 |
| C、有一正根一负根且正根绝对值大 |
| D、有一正根一负根且负根绝对值大 |
考点:根与系数的关系,根的判别式
专题:
分析:根据根的判别式△=b2-4ac的符号,就可判断出一元二次方程的根的情况;由根与系数的关系可以判定两根的正负情况.
解答:解:∵a>0,b<0,c<0,
∴△=b2-4ac>0,
<0,-
>0,
∴一元二次方程ax2+bx+c=0有两个不相等的实数根,且两根异号,正根的绝对值较大.
故选:C.
∴△=b2-4ac>0,
| c |
| a |
| b |
| a |
∴一元二次方程ax2+bx+c=0有两个不相等的实数根,且两根异号,正根的绝对值较大.
故选:C.
点评:此题考查了根的判别式;一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
把抛物线y=(x-1)2+2绕原点旋转180°后得到的图象的解析式为( )
| A、y=-(x+1)2-2 |
| B、y=-(x-1)2-2 |
| C、y=-(x-1)2+2 |
| D、y=-(x+1)2+2 |
下列各组数中互为相反数的一组是( )
| A、1和1 | |||
B、1和-
| |||
C、-1和
| |||
D、-|-1|和-
|
 如图,在△ABC中,AB=AC,点D在AC上,且AD=BD.
如图,在△ABC中,AB=AC,点D在AC上,且AD=BD.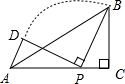 如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于
如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于