题目内容
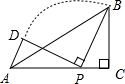 如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于
如图,在△ABC中,∠ACB=90°,AC=5,BC=3,点P是AC边上的一个动点,将线段PB绕着点P逆时针旋转90°,得到线段PD,连接AD,则线段AD的最小值等于考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:
分析:过D作DE⊥AC于E,证△DEP≌△PCB,推出PE=BC=3,DE=CP,设PC=x,则AD2=x2+(2-x)2=2(x-1)2+2,求出即可.
解答:解:
过D作DE⊥AC于E,
∵∠C=∠DPB=90°,
∴∠DEP=∠C=90°,∠EDP+∠DPE=90°,∠DPE+∠BPC=90°,
∴∠EDP=∠BPC,
在△DEP和△PCB中,
,
∴△DEP≌△PCB(AAS),
∴PE=BC=3,DE=CP,
设PC=x,则AD2=x2+(2-x)2=2(x-1)2+2,
∴AD2的最小值是2,
∴AD的最小值是
,
故答案为:
.

过D作DE⊥AC于E,
∵∠C=∠DPB=90°,
∴∠DEP=∠C=90°,∠EDP+∠DPE=90°,∠DPE+∠BPC=90°,
∴∠EDP=∠BPC,
在△DEP和△PCB中,
|
∴△DEP≌△PCB(AAS),
∴PE=BC=3,DE=CP,
设PC=x,则AD2=x2+(2-x)2=2(x-1)2+2,
∴AD2的最小值是2,
∴AD的最小值是
| 2 |
故答案为:
| 2 |
点评:本题考查了全等三角形的性质和判定,旋转的性质,二次函数的最值,勾股定理的应用,关键是得出二次函数的解析式.

练习册系列答案
相关题目
一元二次方程ax2+bx+c=0中,若a>0,b<0,c<0,则这个方程根的情况是( )
| A、有两个正根 |
| B、有两个负根 |
| C、有一正根一负根且正根绝对值大 |
| D、有一正根一负根且负根绝对值大 |
在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,若AD、BC、EF相交于O,OA=OD,OB=OC,点E、F分别在AB、CD上,则OE=
如图,若AD、BC、EF相交于O,OA=OD,OB=OC,点E、F分别在AB、CD上,则OE=