题目内容
4.已知二次函数y=x2+(a+1)x+b(a、b为常数),当x=3时,y=3;当x为任意实数时,都有y≥x,则抛物线的顶点到x轴的距离为( )| A. | $\frac{11}{4}$ | B. | 3 | C. | $\frac{13}{4}$ | D. | 4 |
分析 先把x=3,y=3代入y=x2+(a+1)x+b得到b=-3a-9,则利用当x为任意实数时,都有y≥x得到x2+ax-3a-9≥0,则对于抛物线y=x2+ax-3a-9,它与x轴没有公共点或只有一个公共点,根据△的意义得△=(a+6)2≤0,所以a=-6,b=9,于是得到原抛物线解析式为y=x2-5x+9,把它配成顶点式得到顶点坐标,进而得到抛物线的顶点到x轴的距离.
解答 解:把x=3,y=3代入y=x2+(a+1)x+b得9+3a+3+b=3,则b=-3a-9,
∵当x为任意实数时,都有y≥x,
即x2+(a+1)x+b≥x,
∴x2+(a+1)x-3a-9≥x,即x2+ax-3a-9≥0,
∴抛物线y=x2+ax-3a-9与x轴没有公共点或只有一个公共点,
∴△=a2-4(-3a-9)=(a+6)2≤0,
∴a+6=0,解得a=-6,
∴b=9,
∴y=x2-5x+9=(x-$\frac{5}{2}$)2+$\frac{11}{4}$,
∴抛物线的顶点坐标为($\frac{5}{2}$,$\frac{11}{4}$),
∴抛物线的顶点到x轴的距离为$\frac{11}{4}$.
故选A.
点评 本题主要考查了二次函数的性质,解答本题的关键是利用当x为任意实数时,都有y≥x,求出a的值,此题有一定的难度.

练习册系列答案
相关题目
18.若二次函数$y=m{x^2}+3x+\sqrt{3}$在平面直角坐标系中的图象与x轴有交点,则m的取值范围是( )
| A. | m>$\frac{{3\sqrt{3}}}{4}$ | B. | m≤$\frac{{3\sqrt{3}}}{4}$且m≠0 | C. | m>$\frac{{\sqrt{3}}}{4}$ | D. | m≤$\frac{{\sqrt{3}}}{4}$且m≠0 |
14.抛物线y=x2-2x-1与坐标轴交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
9.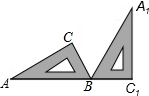 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
14.将一个正方形桌面砍去一个角后得到的桌面是( )
| A. | 五边形 | B. | 四边形 | C. | 三边形 | D. | 以上都有可能 |
 度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).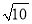 时运动时间t的值;
时运动时间t的值;