题目内容
14.抛物线y=x2-2x-1与坐标轴交点个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 当x=0时,求出与y轴的纵坐标;当y=0时,求出与x轴的交点横坐标,从而求出与坐标轴的交点.
解答 解:当x=0时,y=-1,
则与y轴的交点坐标为(0,-1);
当y=0时,x2-2x-1=0,
△=8>0.
则与x轴有两个交点;
综上所述,抛物线y=x2-2x-1与坐标轴一共有3个交点.
故选:D.
点评 本题考查了抛物线与坐标轴的交点坐标,分别令x=0,y=0,将抛物线转化为方程是解题的关键.

练习册系列答案
相关题目
6.已知一次函数y=kx+3,当x=-1时,y=-1,那么当x=1时,y等于( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
3.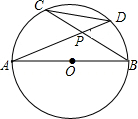 已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
 已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )| A. | sin∠APC | B. | cos∠APC | C. | tan∠APC | D. | $\frac{1}{tan∠APC}$ |
19.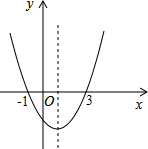 如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )
如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )
 如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )
如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )| A. | abc<0 | B. | 当x>1时,y随x值的增大而增大 | ||
| C. | a+b+c>0 | D. | 当y>0时,-1<x<3 |
4.已知二次函数y=x2+(a+1)x+b(a、b为常数),当x=3时,y=3;当x为任意实数时,都有y≥x,则抛物线的顶点到x轴的距离为( )
| A. | $\frac{11}{4}$ | B. | 3 | C. | $\frac{13}{4}$ | D. | 4 |
2.下列关于有序数对的说法正确的是( )
| A. | (3,2)与(2,3)表示的位置相同 | |
| B. | (a,b)与(b,a)表示的位置一定不同 | |
| C. | (3,-2),(-2,3)是表示不同位置的两个有序数对 | |
| D. | (4,4)与(4,4)表示两个不同的位置 |
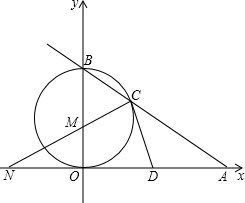 如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.