题目内容
18.若二次函数$y=m{x^2}+3x+\sqrt{3}$在平面直角坐标系中的图象与x轴有交点,则m的取值范围是( )| A. | m>$\frac{{3\sqrt{3}}}{4}$ | B. | m≤$\frac{{3\sqrt{3}}}{4}$且m≠0 | C. | m>$\frac{{\sqrt{3}}}{4}$ | D. | m≤$\frac{{\sqrt{3}}}{4}$且m≠0 |
分析 二次函数图象与x轴有交点,则△=b2-4ac≥0,且m≠0,列出不等式则可.
解答 解:由题意知:
$\left\{\begin{array}{l}{{3}^{2}-4\sqrt{3}m≥0}\\{m≠0}\end{array}\right.$,
解得m≤$\frac{3\sqrt{3}}{4}$且m≠0.
故选:B.
点评 该题考查了函数图象与坐标轴的交点判断,当△=b2-4ac>0时图象与x轴有两个交点;当△=b2-4ac=0时图象与x轴有一个交点;当△=b2-4ac<0时图象与x轴没有交点.

练习册系列答案
相关题目
3.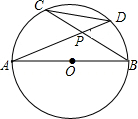 已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
 已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )
已知:如图,AB是⊙O的直径,弦AD、BC相交于P点,那么$\frac{DC}{AB}$的值为( )| A. | sin∠APC | B. | cos∠APC | C. | tan∠APC | D. | $\frac{1}{tan∠APC}$ |
4.已知二次函数y=x2+(a+1)x+b(a、b为常数),当x=3时,y=3;当x为任意实数时,都有y≥x,则抛物线的顶点到x轴的距离为( )
| A. | $\frac{11}{4}$ | B. | 3 | C. | $\frac{13}{4}$ | D. | 4 |
 如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.
如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.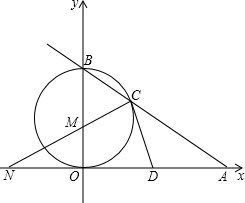 如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.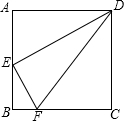 如图所示,已知正方形ABCD的周长为16cm,E为AB的中点,F为BC上一点,且BF:FC=1:3,求△DEF的周长和面积.
如图所示,已知正方形ABCD的周长为16cm,E为AB的中点,F为BC上一点,且BF:FC=1:3,求△DEF的周长和面积.