题目内容
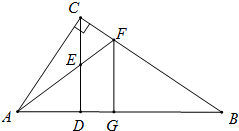 如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,E是CD的中点,AE的延长线交BC于点F,FG⊥AB于点G,求证:FG2=FC•FB.
如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,E是CD的中点,AE的延长线交BC于点F,FG⊥AB于点G,求证:FG2=FC•FB.考点:相似三角形的判定与性质
专题:证明题
分析:延长AC,GF相交于点H,可得到△HCF∽△BGF,由相似的性质得到
=
,即CF•BF=FG•HF,然后只要证明FG=HF即可.
| CF |
| FG |
| HF |
| BF |
解答:证明:延长AC,GF相交于点H,
∵FG⊥AB(已知)
∴∠FGB=90°(垂直的定义)
∵∠ACB=90°(已知)
∴∠FGB=∠ACB(等量代换)
∵∠1=∠2(对顶角相等)
∴△HCF∽△BGF(两角对应相等的两个三角形相似)
∴
=
(相似三角形对应边成比例)
即CF•BF=FG•HF(比例的基本性质)
∵CD⊥AB,FG⊥AB(已知)
∴∠4=∠5=90°(垂直的定义)
∴CD∥HG(同位角相等,两直线平行)
∴∠3=∠H(两直线平行,同位角相等)
∵∠3=∠H,∠6=∠6
∴△ACE∽△AHF(两角对应相等的两个三角形相似)
∴
=
(相似三角形对应边成比例)
∵∠4=∠5,∠7=∠7
∴△AED∽△AFG(两角对应相等的两个三角形相似)
∴
=
(相似三角形对应边成比例)
∴
=
(等量代换)
∵E是CD的中点(已知)
∴CE=DE(中点的定义)
∴FH=FG
∵CF•BF=FG•HF(已证)
∴CF•BF=FG•FG
即FG2=FC•FB.
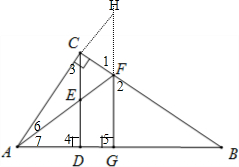
∵FG⊥AB(已知)
∴∠FGB=90°(垂直的定义)
∵∠ACB=90°(已知)
∴∠FGB=∠ACB(等量代换)
∵∠1=∠2(对顶角相等)
∴△HCF∽△BGF(两角对应相等的两个三角形相似)
∴
| CF |
| FG |
| HF |
| BF |
即CF•BF=FG•HF(比例的基本性质)
∵CD⊥AB,FG⊥AB(已知)
∴∠4=∠5=90°(垂直的定义)
∴CD∥HG(同位角相等,两直线平行)
∴∠3=∠H(两直线平行,同位角相等)
∵∠3=∠H,∠6=∠6
∴△ACE∽△AHF(两角对应相等的两个三角形相似)
∴
| AE |
| AF |
| CE |
| FH |
∵∠4=∠5,∠7=∠7
∴△AED∽△AFG(两角对应相等的两个三角形相似)
∴
| AE |
| AF |
| DE |
| GF |
∴
| CE |
| FH |
| DE |
| FG |
∵E是CD的中点(已知)
∴CE=DE(中点的定义)
∴FH=FG
∵CF•BF=FG•HF(已证)
∴CF•BF=FG•FG
即FG2=FC•FB.

点评:本题主要考查了相似三角形的判定方法与性质,通过作辅助线证明三角形全等,由全等三角形的对应边成比例,列出比例式,进而得出结论.

练习册系列答案
相关题目
某市2012年有人口100万,2013年人口增长率为5%,“单独二胎“政策开放后,预计今年人口增长率约为7%,若2013,2014年人口年平均增长率为x,则( )
| A、x=6% | B、x>6% |
| C、x<6% | D、不能确定 |
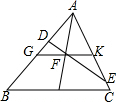 如图,D、E分别是AB、AC上的点,
如图,D、E分别是AB、AC上的点,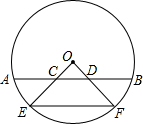 在⊙O中,弦AB∥EF,连结OE、OF交AB于C、D,求证:AC=DB.
在⊙O中,弦AB∥EF,连结OE、OF交AB于C、D,求证:AC=DB.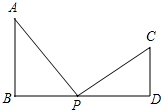 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由B点向D点移动.当P点移动到离B点多远时,△ABP∽△CPD?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由B点向D点移动.当P点移动到离B点多远时,△ABP∽△CPD?