题目内容
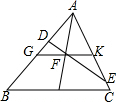如图，D、E分别是AB、AC上的点，| AD |
| AC |
| AE |
| AB |
| 5 |
| 3 |
考点：相似三角形的判定与性质
专题：
分析：由
=
=
，且∠DAE=∠CAB，可证得△ADE∽△ACB，所以∠ADE=∠ACB，再由∠BAF=CAH可证得△ADF∽△ACH
=
=
，再由GK∥BC，可知
=
=
，把BC的值代入可求得GK．
| AD |
| AC |
| AE |
| AB |
| 5 |
| 3 |
| AF |
| AH |
| AD |
| AC |
| 3 |
| 5 |
| GK |
| BC |
| AF |
| AH |
| 3 |
| 5 |
解答：解：
∵由
=
=
，且∠DAE=∠CAB，
∴△ADE∽△ACB，
∴∠ADE=∠ACB，
又∵AH为角平分线，
∴∠BAF=CAH，
∴△ADF∽△ACH，
∴
=
=
，
∵GK∥BC，
∴
=
=
，
∵BC=20cm，
∴
=
，
∴GK=12．
∵由
| AD |
| AC |
| AE |
| AB |
| 5 |
| 3 |
∴△ADE∽△ACB，
∴∠ADE=∠ACB，
又∵AH为角平分线，
∴∠BAF=CAH，
∴△ADF∽△ACH，
∴
| AF |
| AH |
| AD |
| AC |
| 3 |
| 5 |
∵GK∥BC，
∴
| GK |
| BC |
| AF |
| AH |
| 3 |
| 5 |
∵BC=20cm，
∴
| GK |
| 20 |
| 3 |
| 5 |
∴GK=12．
点评：本题主要考查三角形相似的判定和性质，解题的关键是能利用条件两次证得三角形相似，从而得到GK和BC的比值．
练习册系列答案
名校课堂系列答案
相关题目
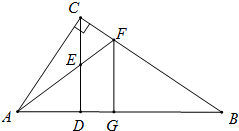如图所示，△ABC中，∠ACB=90°，CD⊥AB于点D，E是CD的中点，AE的延长线交BC于点F，FG⊥AB于点G，求证：FG2=FC•FB．
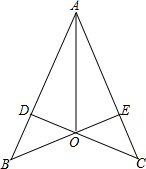如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O，∠BAO=∠CAO，求证：OB=OC．
如图，已知AB、MN与CD相交于点O，OA=OB，OM=ON，试判断∠D与∠C的关系，并说明理由．