题目内容
4个球队进行单循环(所有参加比赛球队,每一队都与其他各队比赛一次),总共比赛的场次是多少?现有8个球队进行比赛,总共需要赛几场?m个球队呢?
考点:规律型:数字的变化类
专题:
分析:利用单循环比赛场数变化规律,进而求出即可.
解答:解:4个球队进行单循环(所有参加比赛球队,每一队都与其他各队比赛一次),
总共比赛的场次是:
×4×3=6(场),
现有8个球队进行比赛,总共需要比赛的场次是:
×8×7=28(场),
m个球队进行比赛,总共需要比赛的场次是:
×m×(m-1)=
(场),
答:4个球队总共比赛的场次是6;现有8个球队进行比赛,总共需要赛28场,m个球队需要
场.
总共比赛的场次是:
| 1 |
| 2 |
现有8个球队进行比赛,总共需要比赛的场次是:
| 1 |
| 2 |
m个球队进行比赛,总共需要比赛的场次是:
| 1 |
| 2 |
| m(m-1) |
| 2 |
答:4个球队总共比赛的场次是6;现有8个球队进行比赛,总共需要赛28场,m个球队需要
| m(m-1) |
| 2 |
点评:此题主要考查了数字变化规律,利用单循环比赛与双循环比赛的区别得出是解题关键.

练习册系列答案
相关题目
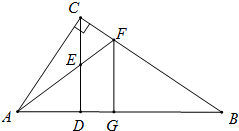 如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,E是CD的中点,AE的延长线交BC于点F,FG⊥AB于点G,求证:FG2=FC•FB.
如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,E是CD的中点,AE的延长线交BC于点F,FG⊥AB于点G,求证:FG2=FC•FB.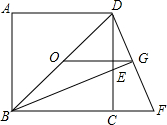 如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG. 如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF.
如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF.