题目内容
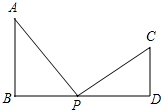如图，AB⊥BD，CD⊥BD，AB=6cm，CD=4cm，BD=14cm，点P在BD上由B点向D点移动．当P点移动到离B点多远时，△ABP∽△CPD？考点：相似三角形的判定
专题：
分析：设出BP=xcm，由BD-BP=PD表示出PD的长，若△ABP∽△PDC，根据相似三角形的对银边成比例可得比例式，把各边的长代入即可列出关于x的方程，求出方程的解即可得到x的值，即为PB的长．
解答：解：由AB=6cm，CD=4cm，BD=14cm，
设BP=xcm，则PD=（14-x）cm，
若△ABP∽△PDC，
∴
=
，
即
=
，
变形得：14x-x2=24，即x2-14x+24=0，
因式分解得：（x-2）（x-12）=0，
解得：x1=2，x2=12，
∴BP=2cm或12cm时，△ABP∽△PDC；
若△ABP∽△CDP，
=
，
即
=
，解得：x=8.4，
∴BP=8.4cm，
综上，BP=2cm或12cm或8.4cm时，△ABP∽△PDC．
设BP=xcm，则PD=（14-x）cm，
若△ABP∽△PDC，
∴
| AB |
| PD |
| BP |
| DC |
即
| 6 |
| 14-x |
| x |
| 4 |
变形得：14x-x2=24，即x2-14x+24=0，
因式分解得：（x-2）（x-12）=0，
解得：x1=2，x2=12，
∴BP=2cm或12cm时，△ABP∽△PDC；
若△ABP∽△CDP，
| AB |
| CD |
| BP |
| DP |
即
| 6 |
| 4 |
| x |
| 14-x |
∴BP=8.4cm，
综上，BP=2cm或12cm或8.4cm时，△ABP∽△PDC．
点评：此题考查了相似三角形的判定与性质，相似三角形的性质有相似三角形的对应边成比例，对应角相等；相似三角形的判定方法有：1、两对对应角相等的两三角形相似；2、两对对应边成比例且夹角相等的两三角形相似；3、三边对应成比例的两三角形相似，本题属于条件开放型探究题，其解法：类似于分析法，假设结论成立，逐步探索其成立的条件．
练习册系列答案
相关题目
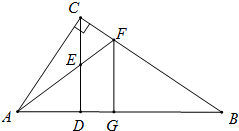如图所示，△ABC中，∠ACB=90°，CD⊥AB于点D，E是CD的中点，AE的延长线交BC于点F，FG⊥AB于点G，求证：FG2=FC•FB．
如图，已知AB、MN与CD相交于点O，OA=OB，OM=ON，试判断∠D与∠C的关系，并说明理由．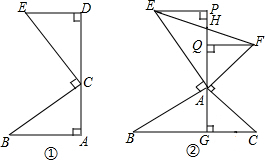
（1）如图①，已知点C在线段AD上，∠BAC=∠BCE=∠EDC=90°，BC=EC，则AB=
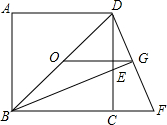如图，O是正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连结DF，交BE的延长线于点G，连结OG．