题目内容
6.将平面直角坐标系中的点P(-2,3),绕坐标原点O顺时针旋转90°,到达点P′,则点P′的坐标是( )| A. | (2,3) | B. | (2,-3) | C. | (-3,-2) | D. | (3,2) |
分析 首先过P作PC⊥y轴于C,过P′作P′D⊥y轴于D,然后证明△PC0≌△P′DO,可得P′D=PC=2,OD=C0=3,进而可得答案.
解答  解:过P作PC⊥y轴于C,过P′作P′D⊥y轴于D.
解:过P作PC⊥y轴于C,过P′作P′D⊥y轴于D.
∵∠POP′=90°,∠COD=90°,
∴∠POC+∠P′OC=90°,∠P′OD+∠P′OC=90°,
∴∠POC=∠P′OD,
∵∠PCO=∠P′DO=90°,OP=OP′,
在△PCO和△P′DO中$\left\{\begin{array}{l}{∠PCO=∠P′DO}\\{∠POC=∠P′OD}\\{PO=P′O}\end{array}\right.$,
∴△PC0≌△P′DO(AAS),
∴P′D=PC=2,OD=C0=3,
∴P′的坐标是(3,2).
故选:D.
点评 此题主要考查了旋转的性质,以及全等三角形的判定和性质,关键是掌握旋转后对应线段相等.

练习册系列答案
相关题目
18.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
(1)若工厂生产成本不多于35万元,且获利多于15万元,问工厂有哪几种生产方案?
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
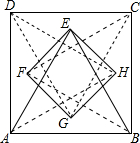 如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.
如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$. 如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)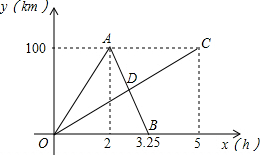 甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:
甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题: