题目内容
 如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )
如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )| A、60° | B、45° |
| C、40° | D、30° |
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:根据等腰三角形性质和三角形内角和定理求出∠ABC,根据线段垂直平分线求出AD=BD,推出∠ABD=∠A=30°,代入∠DBC=∠ABC-∠ABD求出即可.
解答:解:∵△ABC中,AB=AC,∠A=30°,
∴∠ABC=∠C=
(180°-∠A)=75°,
∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∴∠ABD=∠A=30°,
∴∠DBC=∠ABC-∠ABD=75°-30°=45°,
故选B.
∴∠ABC=∠C=
| 1 |
| 2 |
∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∴∠ABD=∠A=30°,
∴∠DBC=∠ABC-∠ABD=75°-30°=45°,
故选B.
点评:本题考查了等腰三角形性质,三角形内角和定理,线段垂直平分线的应用,解此题的关键是求出∠ABC和∠ABD的度数.

练习册系列答案
相关题目
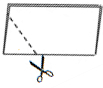 如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )
如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )| A、22.5° | B、45° |
| C、60° | D、135° |
顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
| A、①③ | B、②③ | C、③④ | D、②④ |
 如图,将平行四边形ABCD的边BC延长,若∠A=110°,则∠1=( )
如图,将平行四边形ABCD的边BC延长,若∠A=110°,则∠1=( )| A、70° | B、80° |
| C、100° | D、110° |
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2015次后,点A( )
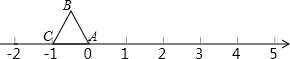
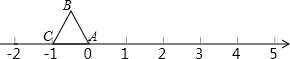
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
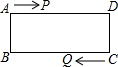 如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是
如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是 如图,在平面直角坐标系中,A(-1,-3),OB=
如图,在平面直角坐标系中,A(-1,-3),OB=