题目内容
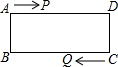 如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是
如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是考点:矩形的性质
专题:动点型
分析:由已知可得:点Q需要4次到达B点,而在每次的运动过程中都有一次PQ∥AB,根据AD∥BC,PQ∥AB,则可知四边形APQB是平行四边形,则当PA=BQ时四边形APQB是平行四边形,列方程求解即可得到所需时间.
解答:解:根据已知可知:点Q将4次到达B点;
在点Q第一次到达点B过程中,
∵四边形ABCD是矩形,
∴AD∥BC,
若PQ∥AB,
则四边形APQB是平行四边形,
∴AP=BQ,
设过了t秒,PQ∥AB,则PA=t,BQ=12-4t,
∴t=12-4t,
∴t=2.4,
在点Q第二次到达点B过程中,
设过了t秒,则PA=t,BQ=4(t-3),
解得:t=4,
在点Q第三次到达点B过程中,
设过了t秒,则PA=t,BQ=12-4(t-6),
解得:t=7.2,
在点Q第四次到达点B的过程中,
设过了t秒,则PA=t,BQ=4(t-9),
解得:t=12(s).
故这段时间内线段PQ有4次与线段AB平行.
故答案为:2.4s或4s或7.2s或12s.
在点Q第一次到达点B过程中,
∵四边形ABCD是矩形,
∴AD∥BC,
若PQ∥AB,
则四边形APQB是平行四边形,
∴AP=BQ,
设过了t秒,PQ∥AB,则PA=t,BQ=12-4t,
∴t=12-4t,
∴t=2.4,
在点Q第二次到达点B过程中,
设过了t秒,则PA=t,BQ=4(t-3),
解得:t=4,
在点Q第三次到达点B过程中,
设过了t秒,则PA=t,BQ=12-4(t-6),
解得:t=7.2,
在点Q第四次到达点B的过程中,
设过了t秒,则PA=t,BQ=4(t-9),
解得:t=12(s).
故这段时间内线段PQ有4次与线段AB平行.
故答案为:2.4s或4s或7.2s或12s.
点评:此题考查了矩形的性质与平行四边形的判定与性质,此题属于运动型题目.此题属于中档题,解题时要注意数形结合与方程思想的应用.

练习册系列答案
相关题目
如图,该图形的相邻两边均互相垂直,则这个图形的周长为( )


| A、37 | B、26 | C、42 | D、21 |
下列方程中是二元一次方程的是( )
| A、x-xy=l | ||
| B、x-2y+z=1 | ||
| C、3x-y=1 | ||
D、
|
 如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )
如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )| A、60° | B、45° |
| C、40° | D、30° |
 观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为
观察图形(左右分别为平移前后两图形),若图中的点P的坐标为(2.6,2),则它在右图中的对应点P1的坐标为 如图,在△ABC中,∠C=90°,∠B=38°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求
如图,在△ABC中,∠C=90°,∠B=38°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求