题目内容
2.在△ABC中,AB=AC,BC=6,△ABC的外接圆的半径为5,求△ABC的面积.分析 分成△ABC是锐角三角形的钝角三角形两种情况进行讨论,作AD⊥BC于点D,则AD一定经过点圆心O,利用垂径定理和勾股定理求得OD的长,则AD即可求得,根据三角形的面积公式求解.
解答 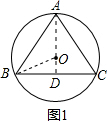 解:当△ABC是锐角三角形时,如图1.
解:当△ABC是锐角三角形时,如图1.
作AD⊥BC于点D,则AD一定经过点圆心O,连接OB.
在直角△OBD中,BD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,则OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{3}}$=4.
则AD=OA+OD=5+4=9,
则S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×9=27;
当△ABC是钝角三角形时,如图2.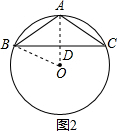
同理,OD=4,则AD=OA-OD=5-4=1,
则S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×1=3.
点评 本题考查了三角形的外接圆,以及垂径定理的应用,注意到分两种情况讨论是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
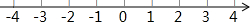 在所给数轴上画出表示数-3,-1$\frac{1}{2}$,|-3$\frac{1}{2}$|,-(-2),0的点,并把这组数从小到大用“<”号连接起来.
在所给数轴上画出表示数-3,-1$\frac{1}{2}$,|-3$\frac{1}{2}$|,-(-2),0的点,并把这组数从小到大用“<”号连接起来.