题目内容
 如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC的中点,AC=6cm,BD=8cm,则OE的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC的中点,AC=6cm,BD=8cm,则OE的长为( )| A、10cm | B、5cm |
| C、2.5cm | D、3cm |
考点:菱形的性质,勾股定理
专题:
分析:由菱形ABCD中,AC=6cm,BD=8cm,根据菱形的性质,可求得AC⊥BD,OB=
BD=4cm,OC=
AC=3cm,然后由勾股定理求得BC的长,又由E是BC的中点,根据直角三角形斜边的中线等于斜边的一半,即可求得OE的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵菱形ABCD中,AC=6cm,BD=8cm,
∴AC⊥BD,OB=
BD=4cm,OC=
AC=3cm,
∴BC=
=5cm,
∵E是BC的中点,
∴OE=
BC=2.5cm.
故选C.
∴AC⊥BD,OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=
| OC2+OB2 |
∵E是BC的中点,
∴OE=
| 1 |
| 2 |
故选C.
点评:此题考查了菱形的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
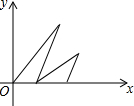 如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )
如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )| A、相同 | ||
B、横向缩短为原来的
| ||
| C、横向拉长为原来的2倍 | ||
| D、横向拉长为原来的4倍 |
下列各式中正确的是( )
| A、-(-a3)4=a12 |
| B、(-an)2=(-a2)n |
| C、(-a-b)3=(a-b)3 |
| D、(a-b)4=(-a+b)4 |
方程2x(x-1)-x(2x-5)=12的解为( )
| A、x=2 | B、x=1 |
| C、x=4 | D、x=0 |
 已知∠AOB=
已知∠AOB=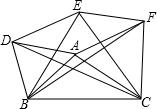 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形. 已知a,b,c在数轴上的对应点如图所示,化简:
已知a,b,c在数轴上的对应点如图所示,化简: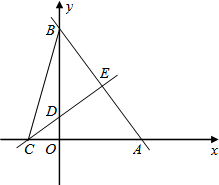 如图,直线y=-
如图,直线y=-