题目内容
18.把二次函数y=x2+bx+c的图象向下平移1个单位长度,再向左平移2个单位长度后,得到的抛物线的顶点坐标为(-1,0),则b+c的值为0.分析 抛物线y=x2+bx+c化为顶点坐标式再按照“左加右减,上加下减”的规律平移则可.
解答 解:根据题意y=x2+bx+c=(x+$\frac{b}{2}$)2+c-$\frac{{b}^{2}}{4}$下平移1个单位,再向左平移2个单位,得y=(x+$\frac{b}{2}$+2)2+c-$\frac{{b}^{2}}{4}$-1.
∵抛物线的顶点坐标为(-1,0),∴-$\frac{b}{2}$-2=-1,c-$\frac{{b}^{2}}{4}$-1=0,
解得:b=-2,c=2,
∴b+c=0,
故答案为:0.
点评 主要考查了函数图象的平移,熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
8.下列调查中,适宜采用普查方式的是( )
| A. | 了解某校初三一班的体育学考成绩 | B. | 了解某种节能灯的使用寿命 | ||
| C. | 了解我国青年人喜欢的电视节目 | D. | 了解全国九年级学生身高的现状 |
13.下列各个实数中,无理数是( )
| A. | 2 | B. | 3.14 | C. | $\frac{7}{13}$ | D. | $\sqrt{2}$ |
3.二零一五年我国与“一带一路”国家贸易额达9955亿美元.数据9955用科学记数法表示为( )
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
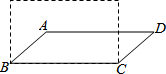 如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°.
如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )